Solucionario COMATEQ 2023
Agradecemos a las universidades que contribuyeron enviando problemas al banco.
P1 (UNICAUCA)
Hallar la mayor potencia de 2 que divida a (24)!.
Nota:
- Los números 2,4,8,16,… son potencias de 2, esto es, son de la forma 2k,k=1,2,3,…
- Para cualquier número natural n≥1, se define n! como
n!=1×2×3×⋯×n.
Find the greatest power of 2 that divides (24)!.
Note:
The numbers 2,4,8,16,… are powers of 2, that is, they have the form 2k,k=1,2,3,…
For any natural number n≥1, n! is defined as
n!=1×2×3×⋯×n.
P2 (UNICAUCA)
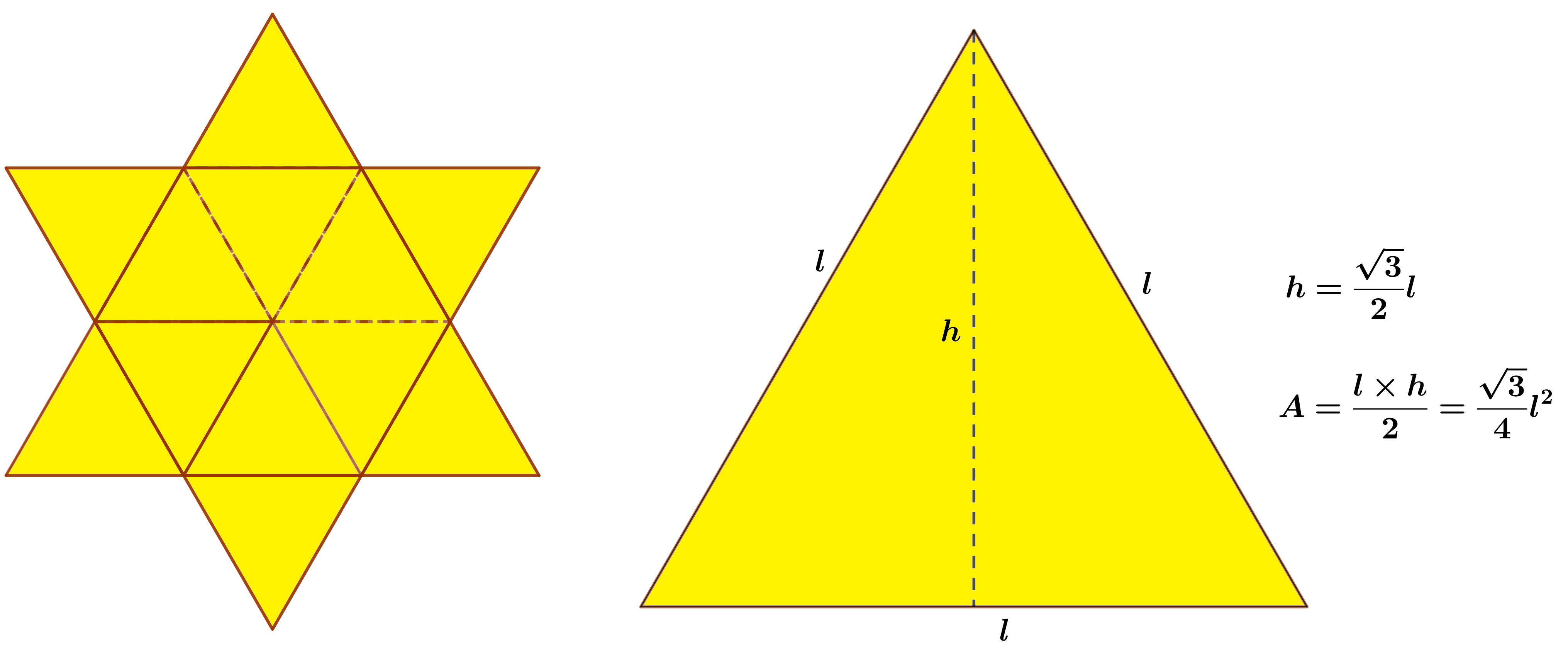
Sobre los lados de un hexágono cuyo lado mide 1cm, se construyen triángulos equilateros, formando así la estrella de David.
Encuentre el área de dicha estrella.
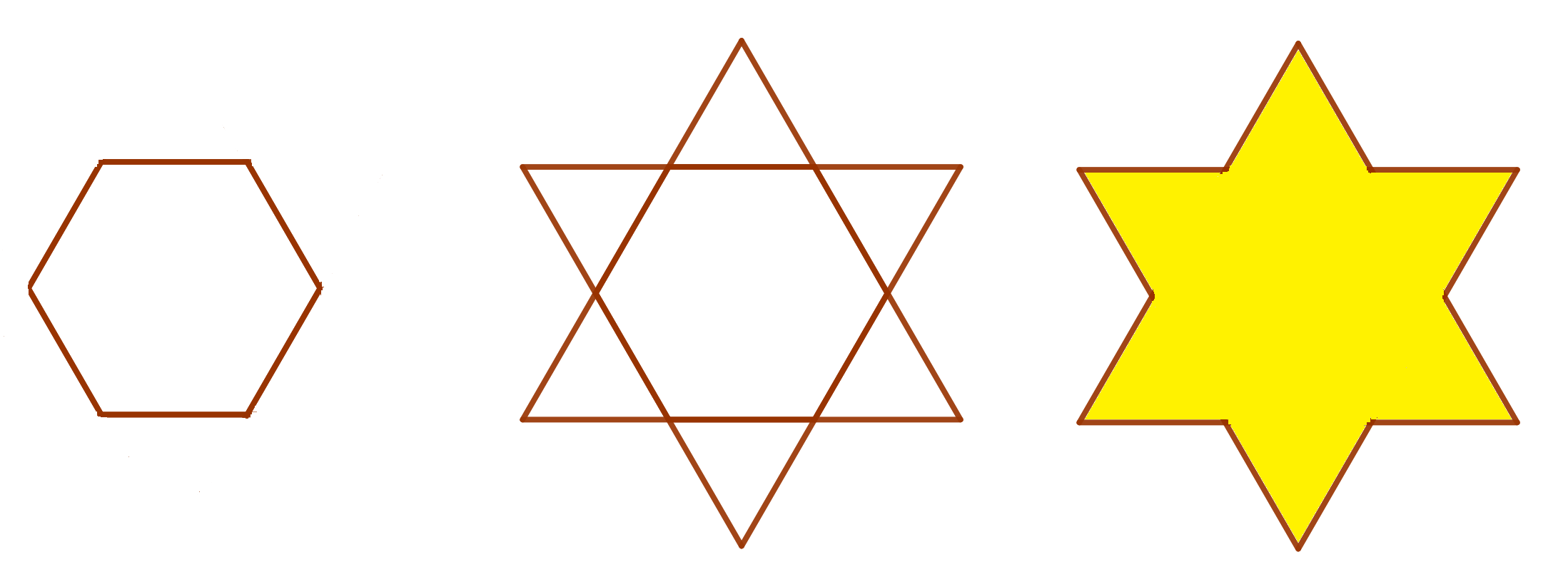
On the sides of a hexagon whose side measures 1cm, equilateral triangles are built, thus forming the Star of David.
Find the area of the star.
P3 (UT)
A Pedro y su padre les agrada jugar a las adivinanzas matemáticas; en esta ocasión Pedro le dijo a su padre la siguiente adivinanza: la suma de dos números es 10 y su producto es 20, adivina cuánto es la suma de sus recíprocos (inversos multiplicativos), ¿cuál es la respuesta que debe dar el padre de Pedro?
Pedro and his father like to play with mathematical riddles; this time Pedro told his father the following riddle: The sum of two numbers is 10 and their product is 20, find out what the sum of their reciprocals (multiplicative inverses) is. What is the answer that Pedro's father should give?
Solución P3
Tenemos el sistema de ecuaciones
x+y=10
x∗y=20
De donde, x=10−y, reemplazando tenemos (10−y)∗y=20, luego
10y−y2=20
−y2+10y−20=0
Usando la fórmula cuadrática para hallar el valor de y,
−10±√102−4(−1)(−20)2(−1)=−10±√100−80−2=−10±√20−2=−10±2√5−2
Por tanto, y puede tomar los siguientes valores:
y1=5−√5 y y2=5+√5, y por consiguiente los valores de x son: x1=5+√5 y x2=5−√5.
Asi pues, la suma de los recíprocos para x1 y y1 es:
1x1+1y1=15+√5+15−√5=(5−√5)+(5+√5)(5+√5)∗(5−√5)=1025−5√5+5√5−5=12
De manera análoga para x2 y y2:
1x2+1y2=15−√5+15+√5=(5+√5)+(5−√5)(5+√5)∗(5−√5)=1025−5√5+5√5−5=12
En ambos casos la respuesta es 12.
Otra solución: Si tenemos que x+y=10 y x∗y=20, y dividimos la 1ra ecuación entre la 2da, obtenemos x+yxy=1y+1x=1020=12.
P4 (UT)
En la feria de juegos hay una nueva atracción, la cual consiste en obtener exactamente 100 puntos en una ruleta con la menor cantidad de tiros posibles. ¿Cuántos tiros puedo hacer para obtener el resultado requerido en el juego?
At the game fair there is a new attraction, which consists of obtaining exactly 100 points in a roulette wheel with the fewest possible shots. How many shots can I take to get the result required in the game?
P5 (UT)
Para la clase de manualidades, Felipe quiere armar un cubo de papel de lado 4 centímetros y su hermano Juan quiere hacer uno más grande y le aumenta el 50% a cada lado del cubo de Felipe. Diga en qué porcentaje aumentó el área superficial del cubo de Juan con respecto al cubo de Felipe.
For the art class, Felipe wants to assemble a paper cube with a side of 4 cm and his brother Juan wants to assemble a biger one and augments by 50% the length of each side in Felipe's cube. Figure out by what percentage did the superficial area of Juan's cube augment relative to Felipe's cube.
Solución P5
Cada lado del cubo de Felipe tiene 4cm, por ende, los lados del cubo de Juan son de 6cm ya que este le aumento el 50% respecto al de su hermano.
El área del cubo de Felipe es la siguiente: A=6∗L2=6∗(4cm)2=96cm2.
Por otro lado, el área del cubo de Juan es: A=6∗62=216cm2
Luego, si x es el porcentaje de aumento del área de un cubo respecto al otro, entonces obtenemos la ecuación: 96+96x%=216, despejando x% tenemos x%=216−9696=1.25 y multiplicando por 100, obtenemos que el porcentaje de aumento es: 125%.
P6 (UNIVALLE)
Un trozo de pastel con forma de cubo de lado 10cm se corta por el plano que pasa por los puntos A, B y C, como muestra la figura, quedando así en dos trozos de diferente tamaño. Encontrar el volumen del trozo más grande.
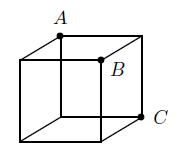
A piece of cake in the shape of a cube with a side of 10cm is cut by the plane that passes through the points A, B y C, as shown in the figure, thus resultinging in two pieces of different sizes. Find the volume of the largest piece.
Solución P6
Observemos que el volumen del trozo de pastel completo es de 10×10×10=1000 centímetros cúbicos. Por otro lado, el trozo más pequeño es una pirámide con base un triángulo isósceles rectángulo cuyos catetos son los lados del cubo. La altura de dicha pirámide es también uno de los lados del cubo.
Usando la formula para el volumen de la pirámide, la cual es
V=13Área de la base×Altura,
tenemos que el área de la base es 1210×10=50cm2. Por tanto el volumen del trozo pequeño es V=1350×10cm3=5003cm3.
Asi que el volumen total de el trozo más grande es
1000−5003=25003cm3.
P7 (UDEA)
El robot en la figura debe de ir de la ciudad en la que está hasta la otra que muestra la figura. Si solo se puede mover de izquierda a derecha y de abajo hacia arriba, ¿cuántos caminos puede tomar en el plano cuadriculado si no puede pasar por la esquina de la roca que se muestra?
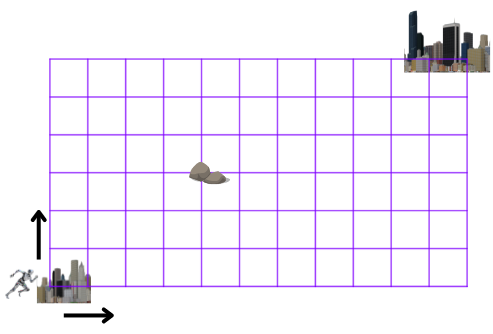
The robot in the figure must go from the city it is in to the other city shown in the figure. If it can only move right or up, how many paths can it take in the square lattice if it cannot go through the intersection with the rock, shown in the figure?
Solución P7
Para contar los caminos que hay de la ciudad del robot hasta la otra, se debe saber que para ir por cualquiera de los caminos se tienen que recorrer 17 calles, 11 horizontales y 6 verticales. y se debe elegir por donde se va a la derecha o por donde se sube. Por lo tanto, el número de formas que hay de ir de la ciudad del robot a la ciudad siguiente es \binom{17}{6}.
El caso anterior no considera el paso por la esquina de la roca, que no se puede. Asi que se debe restar la cantidad de caminos que hay para ir hasta la roca que es \binom{7}{3} y a esa cantidad se le multiplica por el número de caminos que hay para ir de la roca a la otra ciudad \binom{10}{3}. Asi que la cantidad de formas para ir de la ciudad del robot a la otra es \binom{17}{6} - \binom{7}{3} \binom{10}{3}.
P8 (TEC)
Omar tiene un número de 4 dígitos que es múltiplo de 11. Se decide modificar el número agregando dígitos cero entre cada dos dígitos del número original y encuentra que también este es múltiplo de 11. ¿Cuántos números de estos hay?
Omar has a 4-digit number that is a multiple of 11. He decides to modify the number by adding zero digits between each two digits of the original number and finds that this is also a multiple of 11. How many of these numbers are there?
P9 (UNIQUINDIO)
Santiago y Esteban apuestan una carrera de 60m; Santiago gana por 10m. Si ellos vuelven a apostar otra carrera de 78m, y si cada niño corre a la misma velocidad con que corrió la primera carrera, ¿por cuántos metros le gana Santiago a Esteban? (escriba sólo un número, sin unidades)
Santiago and Esteban bet on a 60m race; Santiago wins by 10m. If they bet on another 78m race again, and if each boy runs at the same speed with which he ran the first race, by how many meters does Santiago beat Esteban? (write only a number, no units)
P10 (UNICAUCA)
Halle el menor número natural n tal que 2023\times n sea un cuadrado perfecto.
Nota: Un cuadrado perfecto es un número de la foma k^2.
Find the smallest natural number n such that 2023\times n is a perfect square.
Note: A perfect square is a number of the form k^2.
P11 (UNIVALLE)
Un número de más de tres cifras se dice que tiene la propiedad Fibonacci si cada dígito a partir del tercero es la suma de los dos anteriores. Por ejemplo, el 1347 tiene la propiedad Fibonacci, pues el tercer dígito es 4=1+3, y el cuarto es 7=3+4. Encontrar la suma de los dígitos del número más grande con la propiedad de Fibonacci.
A number with more than three digits is said to have the Fibonacci property if every digit starting from the third is the sum of the two previous digits. For example, 1347 has the Fibonacci property, since the third digit is 4=1+3, and the fourth is 7=3+4. Find the sum of the digits of the largest number with the Fibonacci property.
Solución P11
Notemos que los dígitos van creciendo, pues son la suma de los dos anteriores. Así que, para que un número tenga muchos dígitos se necesita que la suma de los dos primeros dígitos sea lo más pequeña posible. Esto se logra cuando el primer dígito es 1 y el segundo es 0, así el número es 10112358, cuya suma de dígitos es 1+0+1+1+2+3+5+8=21.
Analicemos ahora el caso en el que la suma más pequeña para el tercer dígito es 2. Los posibles números son 202246 y 112358. Note entonces que si se hace que el tercer dígito sea más grande, la suma crece rápidamente, lo que significa que el número tendrá menos de ocho dígitos (es decir, será pequeño). Por lo tanto, el número más grande con la propiedad de Fibonacci es 10112358, y la suma de sus dígitos es 21.
P12 (UDEA)
Si p, q y r son números primos tales que p(p+q)=r-150, halle la menor suma p+q+r.
If p, q and r are prime numbers such that p(p+q)=r-150, find the smallest possible sum p+q+r.
Solución P12
Como la parte izquierda de la ecuación es positiva, entonces la parte derecha también lo es, por lo que r>150, lo que significa que r es impar ya que no puede ser 2 y así r-150 es un número impar.
Por ser el lado derecho impar, p es impar y para que p+q sea un número impar, entonces q=2.
Reescribiendo la ecuación se obtiene que p^2+2p=r-150. Pero note que si completa el cuadrado al lado izquierdo se llega a que (p+1)^2=r-149.
Se debe encontrar un primo r mayor que 150, que al restarse con 149, sea igual a un cuadrado o se debe encontrar un primo p que al sumarle 1 y elevarse al cuadrado y sumarle 149, de un primo.
Los primeros números que satisfacen esto son p=11 y r=293.
Por lo tanto: p+q+r=11+2+293=306.