Solucionario COMATEQ 2020
Agradecemos a las universidades que contribuyeron enviando problemas al banco: UPRM, UDENAR, UNINORTE, UNICAUCA, UNISINU, UIS, UT, UNIVALLE.
1. (UPRM)
¿Cuál es la diferencia entre el mayor número y el menor número formados cada uno con tres dígitos diferentes?
What is the difference between the biggest and the smallest three-digit numbers, each formed by different digits?
2. (UDENAR)

3. (UNINORTE)
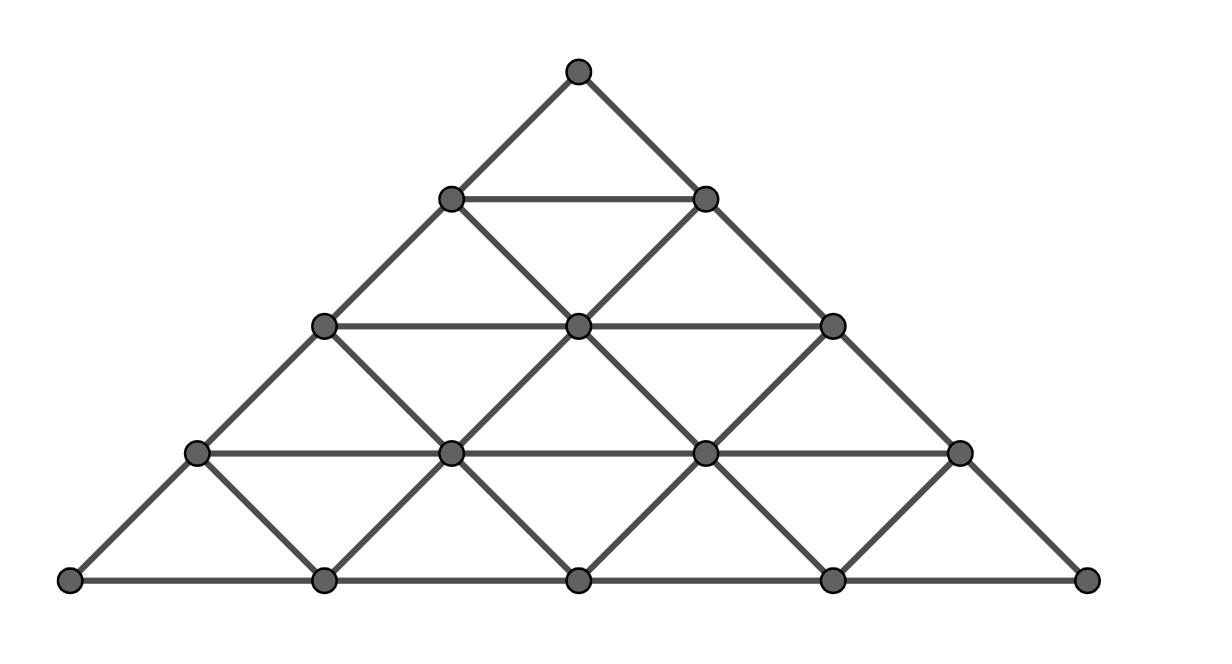
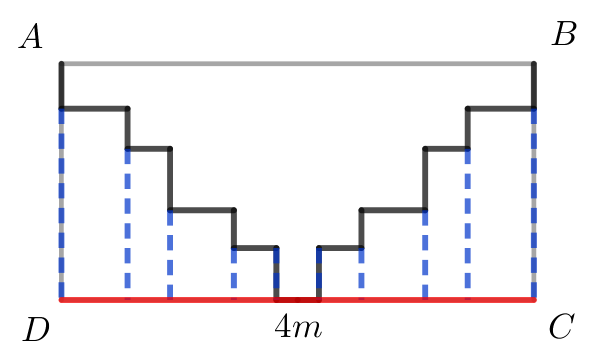
Se desea colorear los vértices en la retícula de la figura de amarillo, azul y rojo de tal manera que no haya dos puntos del mismo color unidos por un segmento. ¿De cuántas maneras es esto posible?
We want to color the vertices of the lattice in the figure yellow, blue and red in such a way that no two points joined by an edge have the same color. In how many ways can we do this?
4. (UNICAUCA)
En la sucesión $$\ldots,a,b,c,d,0,1,1,2,3,5,8,\ldots$$ cada término es la suma de los dos términos inmediatamente a su izquierda. Halle $a$.
In the sequence $$\ldots,a,b,c,d,0,1,1,2,3,5,8,\ldots$$ each term is the sum of the two terms immediately to its left. Find $a$.
5. (UNISINU)
Determine el valor de la variable \(e\) en la siguiente tabla, de modo que la tabla resultante sea un Cuadrado Mágico (es decir, que todas sus filas, columnas y diagonales sumen igual):
| \(1\) | \(15\) | \(14\) | \(4\) |
| \(a\) | \(b\) | \(7\) | \(9\) |
| \(c\) | \(d\) | \(11\) | \(5\) |
| \(e\) | \(f\) | \(g\) | \(h\) |
Determine the value of the variable \(e\) in the following table, such that the resulting table is a Magic Square (i.e. the sum of all its rows, columns and diagonals are equal):
| \(1\) | \(15\) | \(14\) | \(4\) |
| \(a\) | \(b\) | \(7\) | \(9\) |
| \(c\) | \(d\) | \(11\) | \(5\) |
| \(e\) | \(f\) | \(g\) | \(h\) |
Solución
Solución 1:
Como la tabla arriba indicada es un Cuadrado Mágico la suma de sus filas, columnas y diagonales son iguales. Es decir, suman \(34\). Luego tenemos que:
\[\begin{align*}h + 5 + 9 + 4 &=34\\ h &= 16\end{align*}\]
De igual forma \(g=2\) y tenemos la siguiente tabla:
| \(1\) | \(15\) | \(14\) | \(4\) |
| \(a\) | \(b\) | \(7\) | \(9\) |
| \(c\) | \(d\) | \(11\) | \(5\) |
| \(e\) | \(f\) | \(2\) | \(16\) |
De esta última tabla podemos ver que
\[\begin{align*} b+1+11+16&=34 \\ b&=6 \end{align*}\]
Además,
\[\begin{align*} a&=34-22\\ a&=12 \end{align*}\]
Resultando la tabla:
| \(1\) | \(15\) | \(14\) | \(4\) |
| \(12\) | \(6\) | \(7\) | \(9\) |
| \(c\) | \(d\) | \(11\) | \(5\) |
| \(e\) | \(f\) | \(g\) | \(h\) |
Por último, usando la información en la última tabla tenemos el sistema de ecuaciones:
\[\begin{align*} c+d&=34-16\\ c+d&=18 \end{align*}\]
\[\begin{align*} e+f&=34-18\\ e+f&=16 \end{align*} \]
\[\begin{align*} c+e&=34-13\\ c+e&=21\end{align*}\]
\[\begin{align*} d+f&=34-21 \\ d+f&=13\end{align*}\]
\[\begin{align*} e+d&=34-11\\ e+d&=23 \end{align*}\]
De las ecuaciones \(d+e=23\) y \(e+f=16 \) tenemos
\[\begin{align*} d-f&=7 \end{align*}\]
De las ecuaciones \(d+f=13\) y \(d-f=7\), se tiene
\[\begin{align*} 2d&=20\\ d&=10\end{align*}\]
De donde se obtiene que \(f=3\), \(c=8\) y \( e=13\).
Solución 2:
Como la tabla es un Cuadrado Mágico, podemos utilizar el algoritmo para resolver un cuadrado mágico \(4\times 4\) de la siguiente manera.
Se ubican los números del del \(1\) al \(16\) en su orden en la tabla, como sigue:
| \(1\) | \(2\) | \(3\) | \(4\) |
| \(5\) | \(6\) | \(7\) | \(8\) |
| \(9\) | \(10\) | \(11\) | \(12\) |
| \(13\) | \(14\) | \(15\) | \(16\) |
Luego los números en las casillas en blanco se intercambian en parejas de la siguiente forma: \(2\) y \(15\); \(3\) y \(14\); \(5\) y \(12\) y \(8\) y \(9\). Obteniendo la tabla:
| \(1\) | \(15\) | \(14\) | \(4\) |
| \(12\) | \(6\) | \(7\) | \(9\) |
| \(8\) | \(10\) | \(11\) | \(5\) |
| \(13\) | \(3\) | \(2\) | \(16\) |
De donde se obtiene que $ a=12$, $ b=6$, $ c=8$, $ d=10$, $ e=13$, $ f=3$, $ g=2$ y $ h=16$.
6. (UIS)
Juan dibujó un rectángulo que al restarle \(6\) unidades a la base y sumarle \(4\) unidades a la altura se convierte en un cuadrado que tiene la misma área del rectángulo. ¿Cuál es el área rectángulo inicial?
Juan drew a rectangle such that when subtractiing \(6\) units to the base and adding \(4\) units to the height it becomes a square with the same area as the rectangle. What is the area of the initial rectangle?
Solución
Sea \(x\) la base y \(y\) la altura del rectángulo original. Entonces se tiene que
\[(*)\ \ \ \ \ \ x-6=y+4\]
\[(**)\ \ \ \ \ \ xy=(x-6)^{2}\]
De la ecuación \((*)\) se tiene que \(x=y+10,\) de modo que de la ecuación \((**)\) se obtiene \((y+10)y=(y+4)^{2},\) de donde se concluye que \(y=8\) y \(x=18.\) Área del rectángulo es \(8\times 18=144\ u^2.\)
7. (UIS)
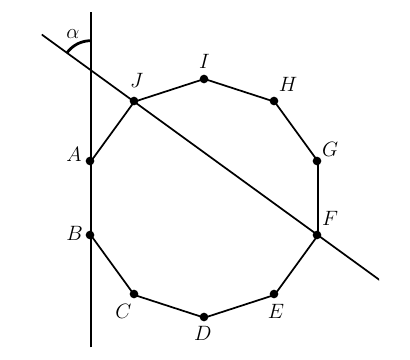
Determinar el valor del ángulo marcado con \(\alpha\) en la siguiente figura, sabiendo que \(ABCDEFGHIJ\) es un decágono regular.
Determine the value of the angle marked with \(\alpha\) in the following figure, knowing that \(ABCDEFGHIJ\) is a regular decagon.
Solución
Considere la siguiente figura en la que \(P\) es la intersección del segmentos \(\overline{ID}\) y \(\overline{JF}\)
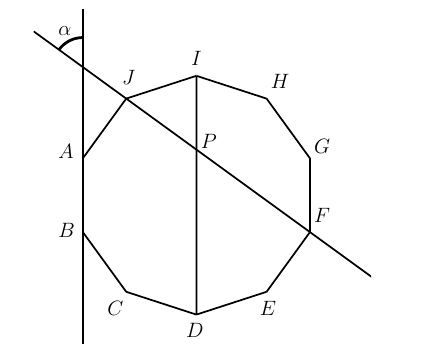
Note que el segmento \(\overline{GF}\) es paralelo a la recta que contiene los puntos \(A\) y \(B\) , luego el ángulo \(\alpha\) es congruente con el ángulo \(GFJ\) por ser ángulos correspondientes entre paralelas. Sabemos que la medida de cada ángulo interno en un decágono regular es \(144°\), y teniendo en cuenta que al trazar todas la diagonales desde un vértice de un polígono regular con \(n\) lados, el ángulo interno del polígono correspondiente a este vértice queda dividido en \(n-2\) ángulos congruentes, se concluye que \(\measuredangle GFJ=\dfrac{144}{8}\times 3=54º\) . Por lo tanto \[\alpha=\measuredangle GFJ=54º.\]
8. (UNICAUCA)
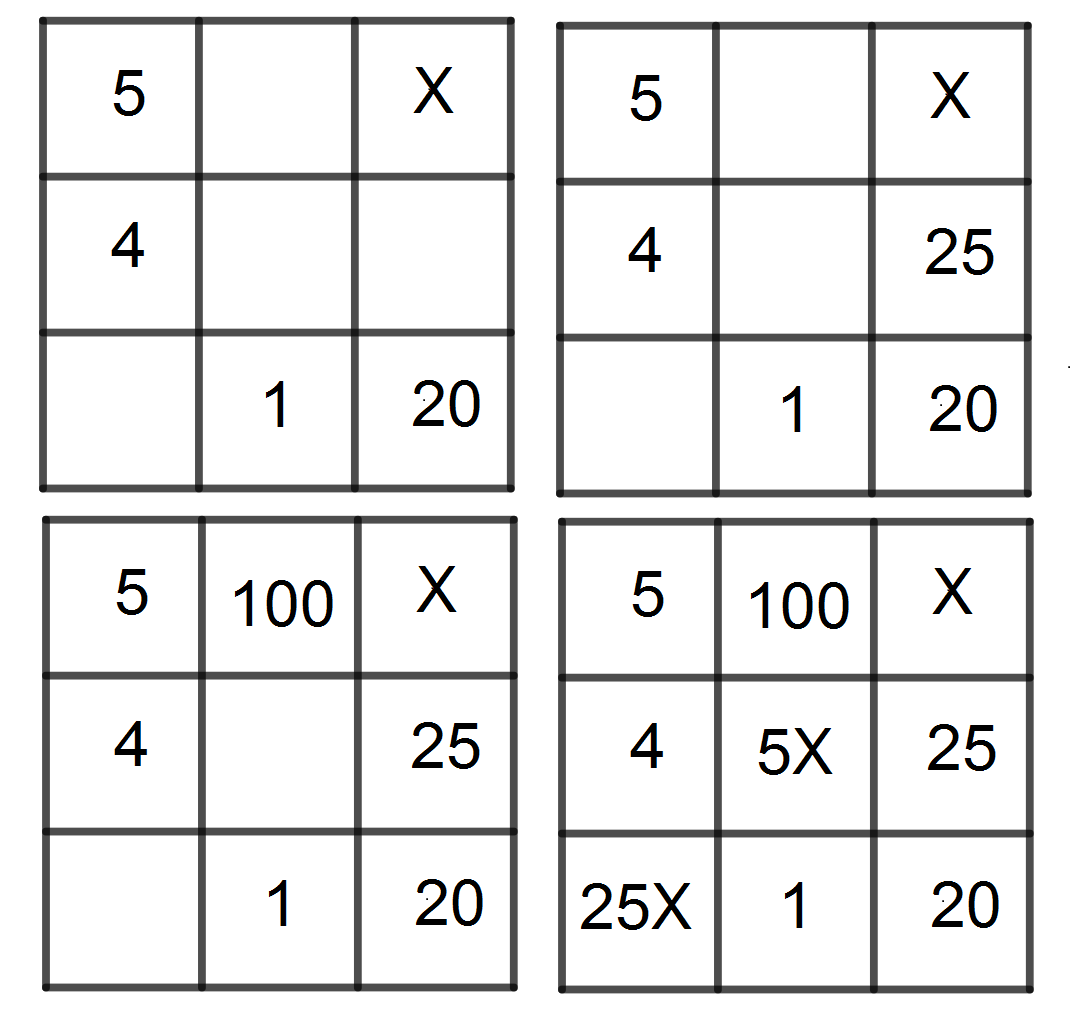
Un cuadrado mágico multiplicativo es tal que el producto de los números en cada fila, columna y diagonal es el mismo. Si las casillas del cuadrado del diagrama se llenan con enteros positivos de modo que se forma un cuadrado mágico multiplicativo, ¿cuál es el valor de $X$?
A multiplicative magic square is such that the product of the numbers in each row, column and diagonal is the same. If the entries in the square are filled with positive integers in such a way that a multiplicative magic square is formed, what is the value of $X$?
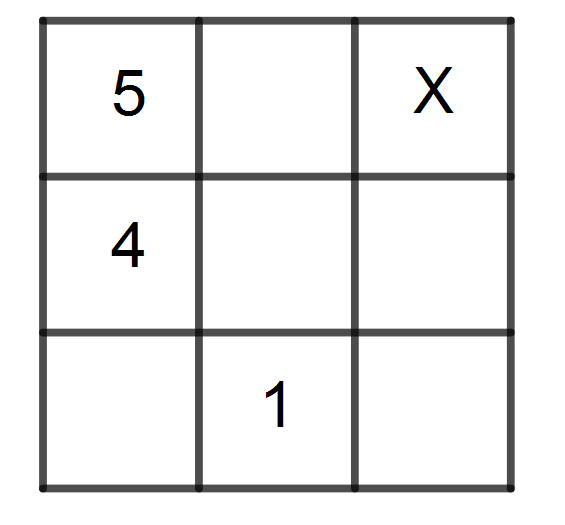
9. (UT)
Se definen las siguientes dos operaciones en los enteros: \(a\circ b= a-b\) y \(a\star b= 3^a+b^4\), calcule \((4\circ 2)\star 3\).
The following two operations are defined in the integers: \(a\circ b= a-b\) and \(a\star b= 3^a+b^4\), calculate \((4\circ 2)\star 3\).
10. (UNIVALLE)
Un número de más de tres cifras se dice que tiene la propiedad Fibonacci si cada dígito a partir del tercero es la suma de los dos anteriores. Por ejemplo, el \(1347\) tiene la propiedad Fibonacci, pues el tercer dígito es \(4=1+3\), y el cuarto es \(7=3+4\). Encontrar la suma de los dígitos del número más grande con la propiedad de Fibonacci.
A number with more than \(3\) digits is said to have the Fibonacci property if each digit starting from the third is the sum of the two previous digits. For example, \(1347\) has the Fibonacci property, since the third digit is \(4=1+3\), and the fourth is \(7=3+4\). Find the sum of all the digits of the largest possible number with the Fibonacci property.
Solución
Notemos que los dígitos van creciendo, pues son la suma de los dos anteriores. Así que, para que un número tenga muchos dígitos se necesita que la suma de los dos primeros dígitos sea lo más pequeña posible. Esto se logra cuando el primer dígito es 1 y el segundo es 0 así el numero es
10112358 cuya suma de dígitos es $1+0+1+1+2+3+5+8=21$.
Observamos que la siguiente suma más pequeña para el tercer dígito es 2, los posibles números son $202246$ y $112358$. Así que si se hace que el tercer dígito sea más grande, la suma crece rápidamente y no hay ningún otro con 8 dígitos, por tanto es el más grande.
11. (UNISINU)
Considere la sucesión de todos los números binarios de \(6\)-dígitos, donde cada uno de los \(6\) dígitos es \(1\) o \(0\). Por ejemplo:
| \(000000\) |
| \(100000\) |
| \(010000\) |
| \(\vdots\) |
| \(111110\) |
| \(111111\) |
Determine cuántos elementos poseen más \(1\)'s que \(0\)'s.
Consider the sequence of all \(6\)-digit binary numbers, where each of the \(6\) digits is \(0\) or \(1\). For example:
| \(000000\) |
| \(100000\) |
| \(010000\) |
| \(\vdots\) |
| \(111110\) |
| \(111111\) |
How many of them have more \(1\)'s than \(0\)'s?
Solución
Solución 1:
Los elementos de la sucesión que poseen más \(1\)'s que \(0\)'s son los que poseen de a cuatro, cinco o seis \(1\)'s. Luego
\[\begin{align*} \binom{6}{4} &= 15\longrightarrow \text{ Cantidad de elementos con cuatro } 1\text{'s} \\ \binom{6}{5} &= 6\longrightarrow \text{ Cantidad de elementos con cinco } 1\text{'s}\\ \binom{6}{6} &= 6\longrightarrow \text{ Cantidad de elementos con seis } 1\text{'s}\\ \end{align*} \]
Por tanto, la cantidad de elementos que poseen más \(1\)'s que \(0\)'s son \(15+6+1=22\).
Solución 2:
La cantidad de elementos en total que tiene la sucesión es \(2^6=64\). Ahora, la cantidad de elementos que tienen igual número de \(1\)'s y \(0\)'s es \({{6}\choose{3}}=20\).
Por simetría la cantidad de elementos que poseen más \(1\)'s que \(0\)'s es la misma cantidad de elementos que poseen más \(0\)'s que \(1\)'s. Por tanto, el número de elementos que tienen más \(1\)'s que \(0\)'s:
\[\frac{2^6 - {{6}\choose{3}}}{2} = \frac{64-20}{2} = \frac{44}{2}=22\]
12. (UDENAR)
Mi clave del banco es "anti-hackers" y consta de siete dígitos que forman un número capicúa, es decir se lee igual de derecha a izquierda que de izquierda a derecha. El primero y los dos últimos dígitos corresponden respectivamente al mes y al día del cumpleaños de mi madre y los tres dígitos del centro (tercera, cuarta y quinta posición) forman un número que es el producto del mes y del día. Si el día del cumpleaños de mi madre es número primo, adivina cuál es la clave que uso.My password at the bank is "anti-hacker" and is made up of seven digits that form a capicúa number, that is, it reads the same from left to right than from right to left. The first and last two digits correspond to the day and month of my mother's birthday and the three middle digits (third, fourth y fifth position) form a number that is the product of that month and day. If the day of my mother's birthday is a prime number, guess my password.

Solución
La clave tiene siete dígitos, enumeramos la posición de cada dígito así: