Solucionario COMATEQ 2017
Agradecemos a las universidades que contribuyeron enviando problemas al banco: UIS, UDEA, UDENAR, UPRM.
1. (UDENAR)
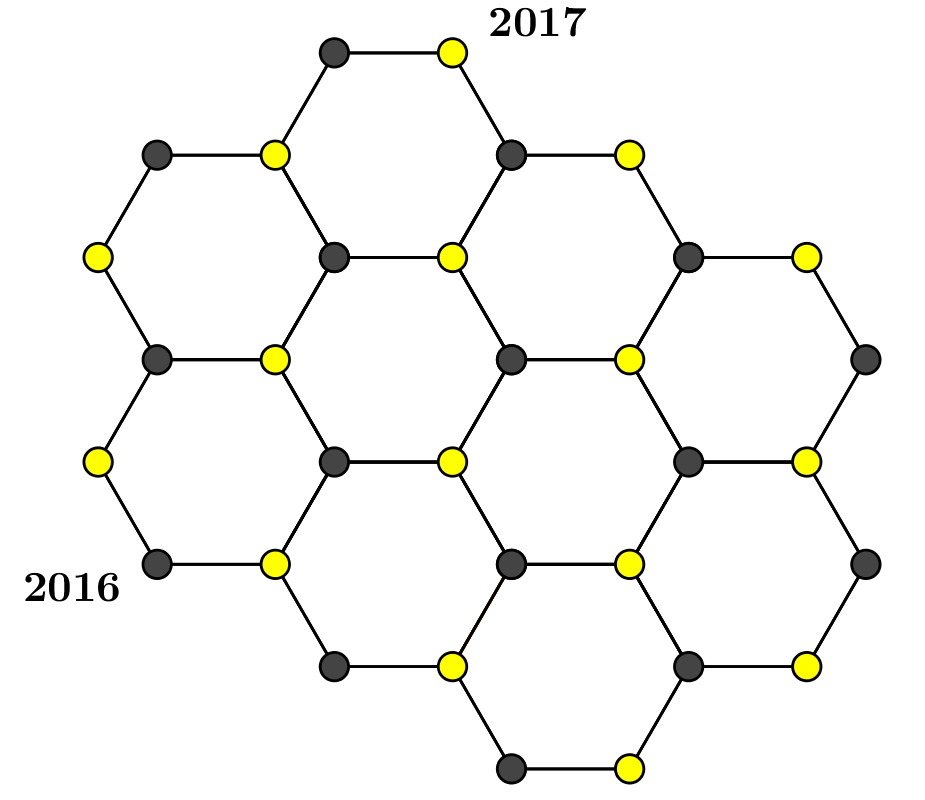
La siguiente figura está construida a partir de hexágonos. Cada vértice en la figura se marca bien sea con 2016 ó 2017. Si se impone la condición de que cada lado de cada hexágono tenga números diferentes y se marcan dos vértices como se muestra en la figura ¿cuál es la diferencia entre la suma de todos los vértices 2017 y la suma de todos los vértices 2016 que aparecerán en la figura?The following figure is constructed using hexagons. Each vertex in the figure is marked with either 2016 or 2017. If the condition that each side of the hexagon should have different numbers is imposed, and two vertices are marked as shown in the figure, what is the difference between the sum of all vertices marked with 2017 and the sum of all vertices marked with 2016 that will appear in the figure?
2. (UPRM)
Una cinta de 18 cm de longitud se corta en tres partes iguales y se elimina el pedazo del medio. A los dos pedazos restantes se les elimina el pedazo del medio. Después a los pedazos restantes se le vuelve a eliminar el pedazo del medio. Si unimos las partes que quedan en una sola cinta, ¿cuánto mide esta nueva cinta?A strip of tape 18 cm long is cut in three equal parts and the middle part is eliminated. Of both remaining parts, the middle third is also eliminated. Then, the middle third part is eliminated from all remaining parts. If we now join together all remaining parts into one strip of tape, what is the length of this new strip of tape?
3. (UDEA)
¿Cuántos cubos dividen al número \(12!=1\times 2\times 3\times \dots \times 11\times 12\)?How many cubes divide the number \(12!=1\times 2\times 3\times \dots \times 11\times 12\)?
4. (UPRM)
Un cuadrado azul tiene un perímetro de \(8\)cm. Un cuadrado rojo tiene un área que es \(9\) veces el área del cuadrado azul. ¿Cuál es el radio del círculo que pasa por los vértices del cuadrado rojo?A blue square has a perimeter of \(8\)cm. A red square has an area that is \(9\) times the area of the blue square. What is the radius of the circle that passes through the vertices of the red square?
5. (UIS)
Los triángulos que cumplan con las siguientes condiciones se llamarán fantásticos:- Todas las longitudes de sus lados son números primos.
- Dos de las longitudes de sus lados deben ser primos gemelos.
- La longitud del lado restante debe ser mayor a la longitud de los otros dos lados.
Nota: Dos números primos son gemelos, si son de la forma \(p\) y \(p+2\).
All triangles satisfying the following conditions are said to be fantastic:
- All the lengths of their sides are prime numbers.
- Two of those lengths have to be twin primes.
- The length of the side that is left must be greater than the length of the other two sides.
Note: Two primes are twin if they are of the form \(p\) and \(p+2\).
Solución
Teniendo en cuenta que los primos gemelos menores que \(50\) son \(\{(3,5), (5,7), (11,13), (17,19), (29,31), (41,43)\}\) y la desigualdad triangular se obtienen las siguientes ternas: \[\begin{align*} &(3,5,7)\\ &(5,7,11)\\ &(11,13,17),\,(11,13,19),\,(11,13,23)\\ &(17,19,23),\,(17,19,29),\,(17,19,31)\\ &(29,31,37),\,(29,31,41),\,(29,31,43),\,(29,31,47)\\ &(41,43,47) \end{align*} \]6. (UDEA)
Si el mínimo común múltiplo entre dos números positivos \(a\) y \(b\) es \(120\) y su máximo común divisor es igual a \(20\), ¿cuál es el menor valor posible de \(a+b\)?If the minimum common multiple of two positive numbers \(a\) and \(b\) is \(120\) and their maximum common divisor is equal to \(20\), what is the least possible value of \(a+b\)?
Solución
Como el \(\text{mcd}(a,b)=20\), por definición tenemos que \(20\) divide \(a\) y \(20\) divide a \(b\), por tanto, existen enteros \(k\) y \(l\) respectivamente tal que \(a=20k\) y \(b=20l\), donde \(k\) y \(l\) son primos relativos. Como sabemos que \[\text{mcd}(a,b)\cdot \text{mcm}(a,b)=a\cdot b.\] Así \(120\cdot 20 = 20k\cdot20l\), que es \(2400=400kl\) y así \(kl=6\), que al factorizar, sin perdidad de generalidad obtenemos que \(k=2\) y \(l=3\) y así \(a=40\) y \(b=60\) y la suma es \(100\).7. (UPRM)
¿Cuál es el dígito de las unidades de \(\frac{2017^{2017}}{\underbrace{2017+2017+...+2017}_{2017-\text{veces}}}\)?What is the unit digit of \(\frac{2017^{2017}}{\underbrace{2017+2017+...+2017}_{2017-\text{times}}}\)?
Solución
\[\begin{align*} \frac{2017^{2017}}{\underbrace{2017+2017+...+2017}_{2017-\text{veces}}} &=\frac{2017^{2017}}{2017 \cdot 2017}\\ &=\frac{2017^{2017}}{2017^2}\\ &=2017^{2015} \end{align*} \] El último dígito de las potencias de \(2017\) tiene el patrón \(7,9, 3, 1, 7, 9, 3, 1,\ldots\). Como \(2015=4\cdot 2003+3\), entonces la respuesta es \(3\).8. (UDENAR)
Cada una de las puntas de un hexagrama, o estrella regular de seis puntas, es un triángulo equilátero. Se puede construir otro hexagrama, usando el punto medio de la base interna de estos triángulos como vértices. Si repetimos este proceso una vez más, se tiene una sucesión de tres hexagramas como se muestra en la figura.¿Cuánto es la suma del área de las puntas de estos hexagramas, si se sabe que el triángulo equilátero más externo es de lado 1?
Each of the tips of a hexagram, or regular six point star, is an equilateral triangle. One can construct another hexagram, using the midpoint of the internal base of these triangles as vertices. If we repeat this process once again, we obtain a sequence of three hexagrams as shown in the figure.
What is the sum of the areas of the tips of these hexagrams, if we know that the most external equilateral triangles have sides of length 1?

Solución
Por simetría, si se identifica el área de uno de los triángulos equiláteros de las puntas de cada hexagrama, se puede obtener el área total \(A\) así:\[A=6A_1+6A_2+6A_3\]
El área del triángulo equilátero de lado 1 es \(A_1=\frac{\sqrt{3}}{4}\), la cual se obtiene usando el Teorema de Pitágoras. Adicionalmente, para formar el primer hexagrama interno, se subdivide cada triángulo equilátero en cuatro triángulos equiláteros de igual área como se muestra en la figura.

El área \(A_2\) de cada uno de estos triángulos es la cuarta parte del área del triángulo \(A_1\), es decir, \(A_2=A_1/4=\sqrt{3}/16\). Realizando nuevamente este proceso, para formar el siguiente hexagrama en la sucesión, se subdivide el triángulo de área \(A_2\) en cuatro triángulos equiláteros iguales y por lo tanto el área de cada uno de estos triángulos es la cuarta parte del área del triángulo \(A_2\). De aquí se sigue que \(A_3=A_2/4=\sqrt{3}/64\). Finalmente, se tiene que el área total es \[A=6A_1+6A_2+6A_3=6\left(\frac{\sqrt{3}}{4}+\frac{\sqrt{3}}{16}+\frac{\sqrt{3}}{64}\right)=63\frac{\sqrt{3}}{32}.\]
9. (UPRM)
Decimos que un número entero es chofito si no es la potencia de un número primo. ¿Cuántos números del 1 al 50 son chofitos?We say an integer number is chofito if it is not the power of a prime number. How many numbers from 1 to 50 are chofitos?
10. (UIS)
Una recta pasa por el punto \((13,0)\) y dista \(5\) unidades del origen del plano cartesiano. ¿Cuál es el área del triángulo que forma dicha recta con los ejes coordenados? Entre su respuesta como una fracción (por ejemplo 13/17) y no entre unidades.A straight line passes through point \((13,0)\) and is \(5\) units away from the origin of the cartesian plane. What is the area of the triangle that this line forms with the coordinate axes? Enter your answer as a fraction (for example 13/17) and do not enter any units.
Solución
Sin pérdida de generalidad consideremos que la recta es la que se muestra en la figura.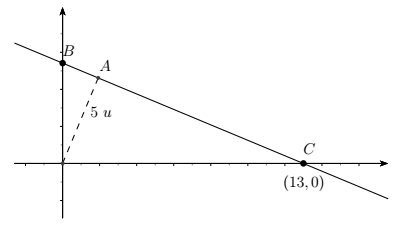
Por Teorema de Pitágoras \(AC=12\) y por semejanza de triángulos \((OA)^2=AB \cdot AC\), luego \(BA=25/12\). Por lo tanto el área del triángulo es: \[\dfrac{\left( \dfrac{25}{12}+12\right) \cdot 5}{2}=\frac{845}{24}.\]
11. (UDENAR)
Las células ROJAS del planeta marte se reproducen cada año, siguiendo la siguiente regla: si el año es par cada célula ROJA genera una célula ROJA y una AZUL, mientras que si el año es impar da lugar a dos células ROJAS. La más reciente investigación de la NASA descubrió que las células ROJAS y AZULES son inmortales, que las células AZULES nunca se reproducen y que cada año toda célula ROJA da vida a nuevas células. Si el 4 de marzo del 2017 un astronauta trajo una célula ROJA recién nacida a nuestro planeta, ¿cuál sería la diferencia (positiva) entre la cantidad de células ROJAS y AZULES el 4 de marzo del 2027?RED cells in the planet Mars reproduce each year, following this rule: if the year is even each RED cell generates one RED cell and one BLUE cell, if the year is odd it generates two RED cells. The most recent research by NASA discovered that the RED and BLUE cells are immortal, that the BLUE cells never reproduce, and that each year all RED cells give life to new cells. If on March 4, 2017 an astronaut brought a newly born RED cell to our planet, what will be the difference (positive) between the amount of RED and BLUE cells on March 4, 2027?
Solución
En la figura se presenta el proceso de reproducción de las células entre los años 2017 y 2022. De donde se obtiene una forma recursiva para la cantidad de células azules y rojas por año.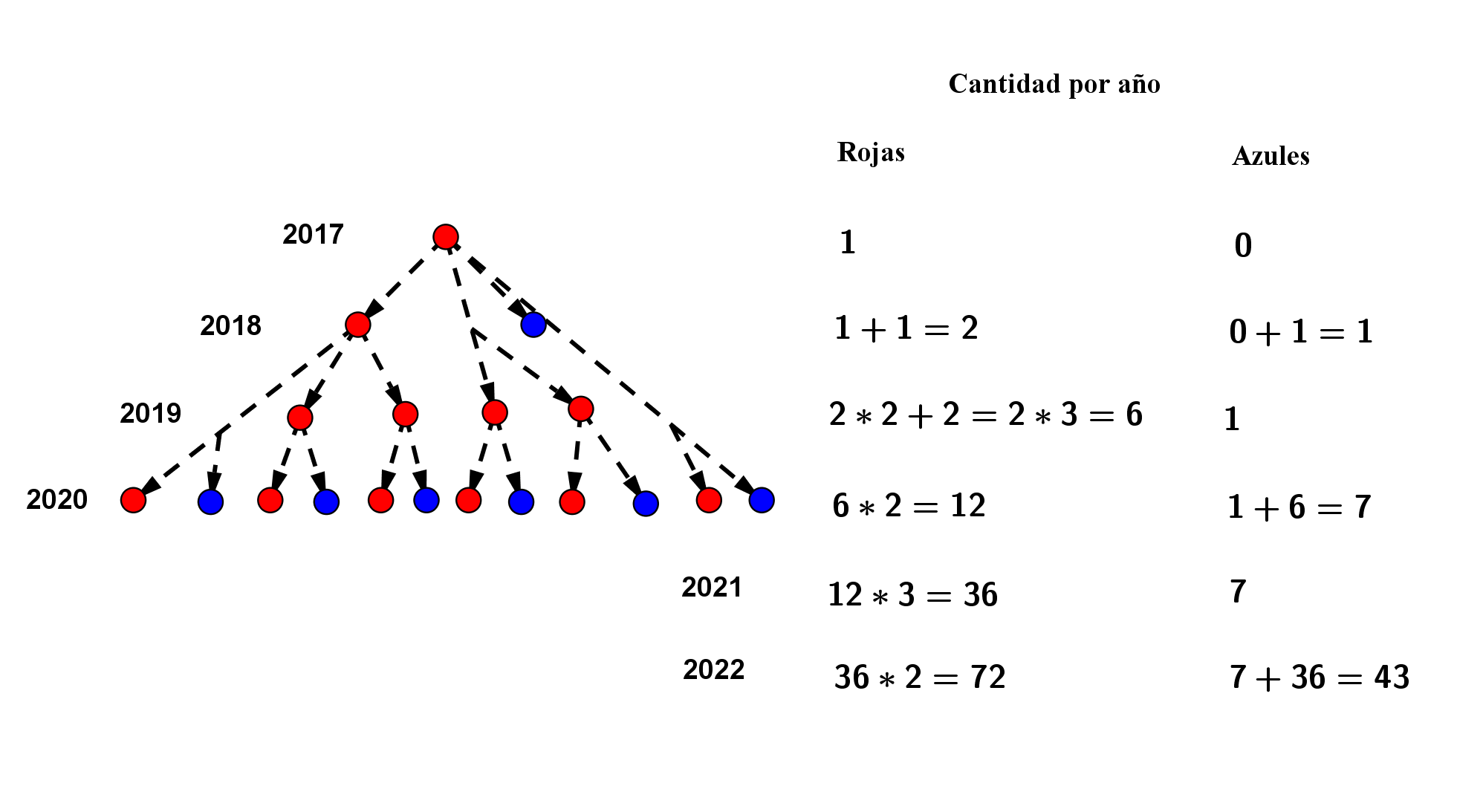 De esta forma al continuar el proceso se concluye que en el año 2027 habrá 7776 células ROJAS y 1555 AZULES. Luego la diferencia entre sus poblaciones será de 6221.
De esta forma al continuar el proceso se concluye que en el año 2027 habrá 7776 células ROJAS y 1555 AZULES. Luego la diferencia entre sus poblaciones será de 6221. 12. (UIS)
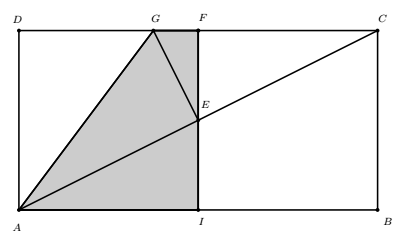
En la siguiente figura \(ABCD\) es un rectángulo donde \(AB=2BC\), \(FC=3 \, cm\), \(F\) es punto medio de \(\overline{DC}\), \(I\) es punto medio de \(\overline{AB}\) y \(\overline{GE}\) es perpendicular a \(\overline{AC}\). Halle el perímetro del cuadrilátero \(AIFG\). Entre la respuesta como una fracción (por ejemplo 13/17) y no entre unidades.In the figure above \(ABCD\) is a rectangle where \(AB=2BC\), \(FC=3 \, cm\), \(F\) is the midpoint of \(\overline{DC}\), \(I\) is the midpoint of \(\overline{AB}\) and \(\overline{GE}\) is perpendicular to \(\overline{AC}\). Find the perimeter of the quadrilateral \(AIFG\). Enter your answer as a fraction (for example 13/17) and do not enter units.