Solucionario COMATEQ 2021
Agradecemos a las universidades que contribuyeron enviando problemas al banco: UDENAR, UNIVALLE, UNICAUCA, UNIQUINDIO, UIS, LUZ
P1 (UDENAR)
Un número es chévere si es a la vez suma de 2 números consecutivos y 3 números consecutivos. ¿Cuántos números entre 2000 y 2021 son chéveres?
A number is chévere if it is both the sum of 2 consecutive numbers and 3 consecutive numbers. How many numbers between 2000 and 2021 are chévere?
S1
Observe que si $n$ es un número chévere, entonces existen enteros $x$ e $y$ tales que \begin{align*} n&=(x-1)+x=2x-1, &\;\rightarrow \text{suma de dos números consecutivos,}\\ n&=(y-1)+y+(y+1)=3y. &\;\rightarrow \text{suma de tres números consecutivos.} \end{align*} De estas dos igualdades, podemos concluir que para que un número sea chévere, debe ser impar y múltiplo de 3. Por lo tanto, existen 4 números chéveres entre 2000 y 2021: 2001, 2007, 2013 y 2019.
P2 (UNIVALLE)
Supongamos que un hexágono regular y un cuadrado comparten un lado como en la figura.
Suppose a regular hexagon and a square share a side as in the figure.
Sean \( A \) el área del hexágono y \( B \) el área del cuadrado. El cociente \( \dfrac{A}{B} \) es igual a
Let \(A \) be the area of the hexagon and \(B \) the area of the square. The quotient \(\dfrac {A} {B} \) is equal to
S2
Sea \( r \) la medida del lado compartido por el hexágono y el cuadrado, tenemos que el área del cuadrado es \( B=r^2 \) y el área del hexágono es \( 6 \) veces el área de un triángulo equilátero de lado \( r\).
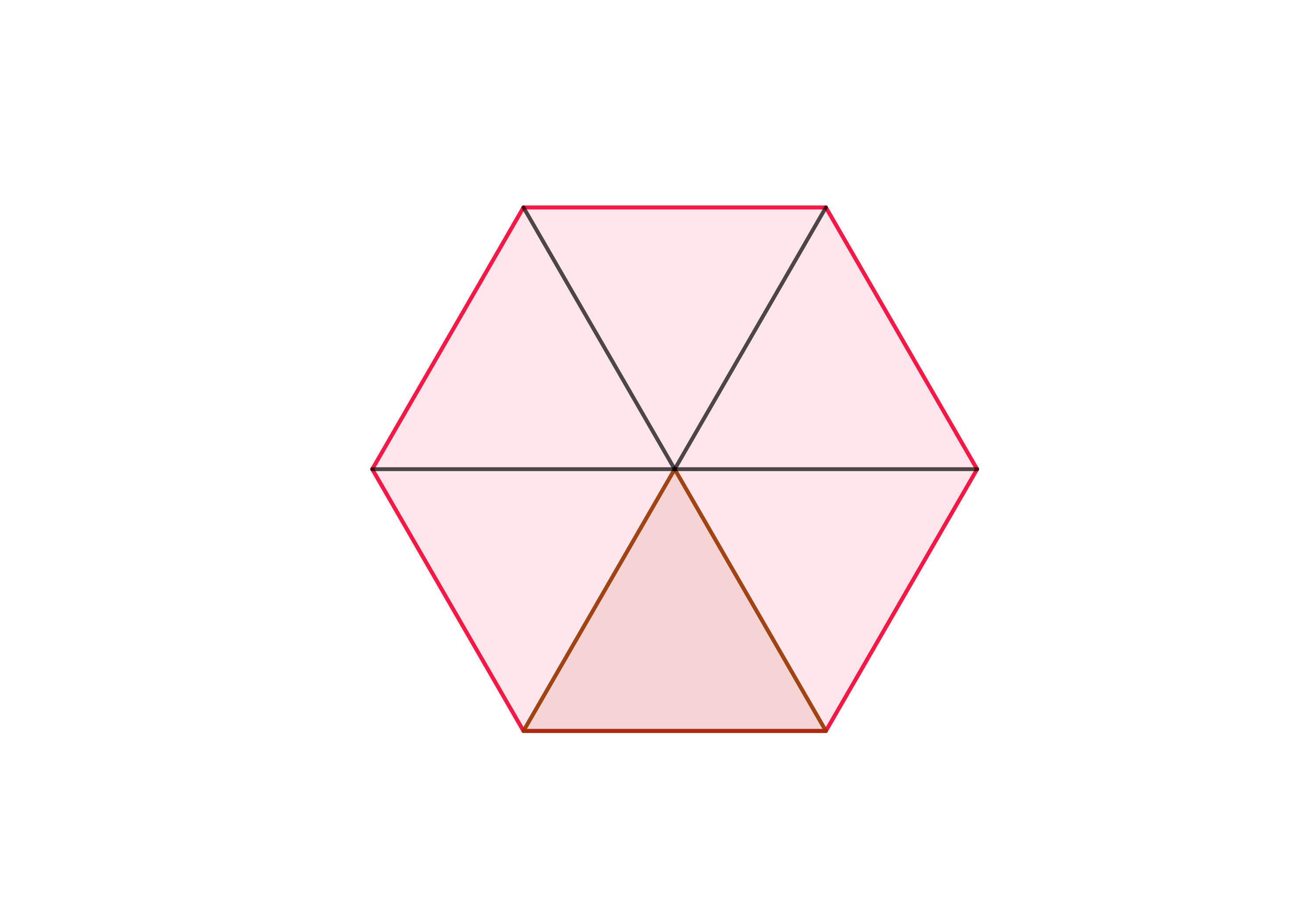
Usando el teorema de Pitagoras obtenemos que la altura de este triángulo es \( \dfrac{\sqrt{3}r}{2} \). Así el área de cada triángulo es \( \dfrac{\sqrt{3}r^2}{4} \) y el área del hexágono es \( A=\dfrac{3\sqrt{3}r^2}{2} \). Concluimos que \( \dfrac{A}{B} = \dfrac{3\sqrt{3}}{2} \).
P3 (UNICAUCA)
Un medicamento cuesta $120. Luego de una disminución del precio, el número de compradores se aumentó en la mitad y el dinero recaudado por la venta aumentó en una cuarta parte. ¿En cuánto se disminuye el precio del medicamento?
A drug costs $120. After a price decrease, the number of buyers was increased by half and the money raised from the sale increased by a quarter. How much is the price of the medicine reduced?
P4 (UNIQUINDIO)
La menor distancia entre las localidades \(A\) y \(B\) separadas por \(5\) montañas encadenadas (una seguida de la otra) que forman triángulos equiláteros con la horizontal es de \(14\) kilómetros.
The smallest distance between the localities \(A \) and \(B \) separated by \(5 \) chained mountains (one followed by the other) that form equilateral triangles with the horizontal is \(14 \) kilometers.
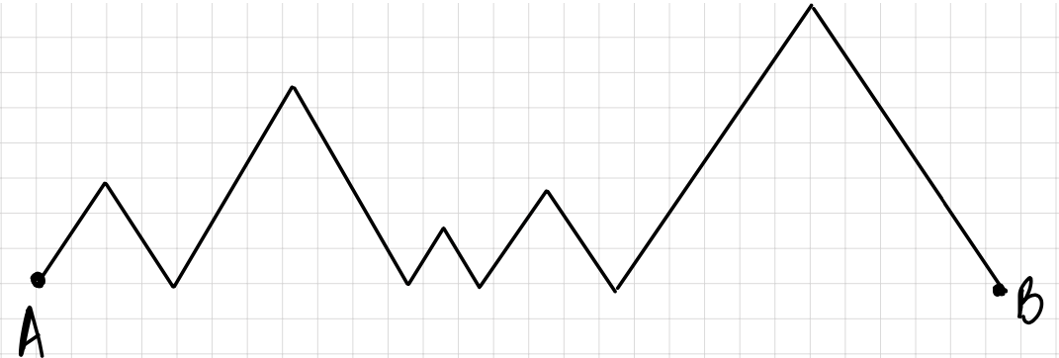
¿Cuál es la distancia que se debe recorrer sobre las montañas para ir de \(A\) hasta \(B\) y regresar?
What is the distance that must be traveled over the mountains to get from \(A \) to \(B \) and back?
P5 (UIS)
Andrea está diseñando el logo de su nuevo emprendimiento, para ello inicia trazando una circunferencia como se muestra a continuación. Si ahora desea inscribir un cuadrado en esta circunferencia, ¿qué área tendrá este cuadrado?
Andrea is designing the logo of her new venture, to do this she begins by drawing a circumference as shown below. If she now wants to inscribe a square on this circumference, what area will this square have?
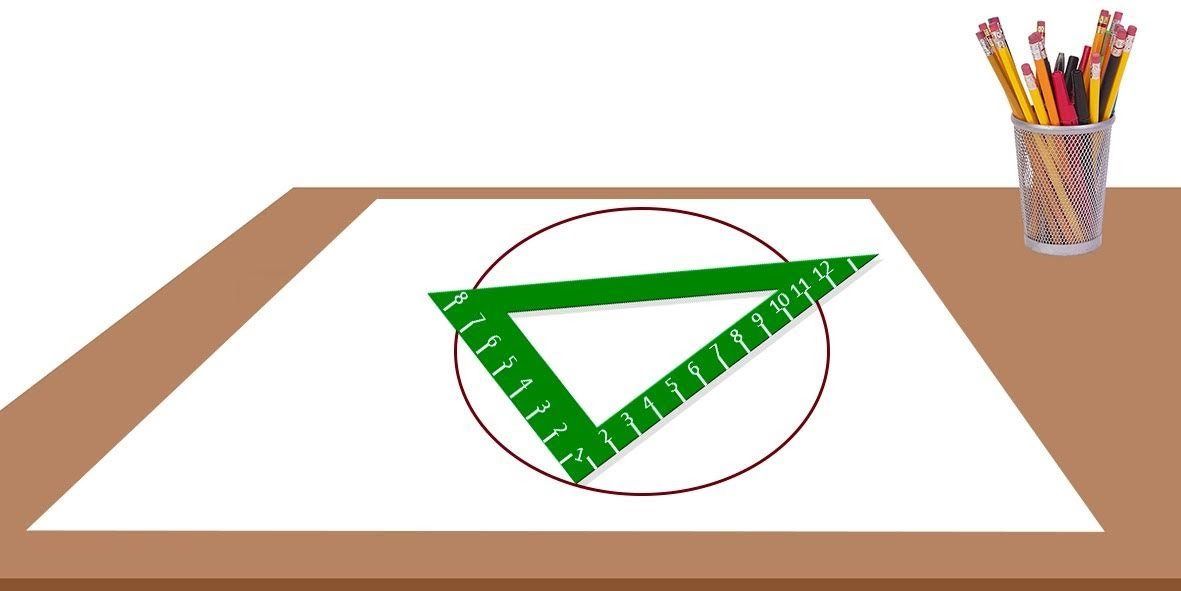
S5
Sean \(A\) el vértice del ángulo recto de la escuadra, \(B\) el punto de intersección de la circunferencia con el lado de la escuadra a los \(7\,cm\) y \(C\) el punto de intersección de la circunferencia con el otro lado de la escuadra a los \(11\,cm.\) Note que el triángulo \(ABC\) es rectángulo en \(A\) y está inscrito en la circunferencia, luego su hipotenusa \(\overline{BC}\) es diámetro de la circunferencia y por el Teorema de Pitágoras, se tiene que
\begin{align*}
BC^2&=7^2+11^2=170.
\end{align*}
Por otro lado, note que al inscribir un cuadrado en una circunferencia, su diagonal coincide con un diámetro de la circunferencia. Sean \(L\) y \(D\) las longitudes del lado y la diagonal de este cuadrado, respectivamente. Por el Teorema de Pitágoras,
\begin{align*}
D^2&=L^2+L^2,\\
L^2&=\dfrac{D^2}{2}.
\end{align*}
De lo anterior se tiene que \(D^2=170,\) por lo tanto el área del cuadrado inscrito es $$L^2=\dfrac{170}{2}=85\,cm^2.$$
P6 (LUZ)
Alrededor de una mesa redonda hay 10 sillas numeradas del 1 al 10. Cinco matrimonios desean sentarse de modo que hombres y mujeres se alternen, pero que ningún hombre quede al lado de su esposa. ¿De cuántas maneras pueden hacerlo?
Around a round table there are 10 chairs numbered from 1 to 10. Five couples want to sit so that men and women alternate, but that no man is next to his wife. In how many ways can they do it?
S6
Los hombres pueden sentarse en las sillas pares o en las impares. Además pueden ordenarse entre ellos de \(5!=120\) maneras. Es decir que pueden sentarse de \(2\times 120 = 240\) maneras. Una vez sentados los hombres, las mujeres pueden sentarse de 13 maneras. Esto puede verse enumerando todas las maneras, o bien aplicando el principio de inclusiones y exclusiones. Así la respuesta es \(240\times 13 = 3120\).
P7 (LUZ)
En un plano se trazan \(n\) rectas diferentes, de modo que no haya tres de ellas concurrentes, es decir, que no se cortan en un mismo punto. Hay 4 de las \(n \) rectas que son paralelas, y no hay ningún otro par de rectas paralelas aparte de los formados por dos rectas de esas cuatro. Si hay 294 puntos de intersección de rectas, ¿cuál es el valor de \(n\)?
On a plane, \(n\) different lines are drawn so that no three of them are concurrent, that is, they do not intersect at the same point. There are 4 of the \(n\) lines that are parallel, and there are no other pairs of parallel lines apart from those formed by two lines of those four. If there are 294 points of intersection of lines, what is the value of \(n\)?
S7
Cada una de las 4 rectas paralelas intersecta a cada una de las \(n-4\) rectas restantes, lo que da \(4(n-4)\) puntos de intersección. Además las \(n-4\) rectas no paralelas se intersectan entre sí en \(\binom{n-4}{2}\) puntos. Por lo tanto
\[ 4(n-4)+\frac{(n-4)(n-5)}{2} = 294, \]
de donde \(n^2-n-600=0\), cuya única raíz positiva es 25.
P8 (UNIVALLE)
¿Cuántos números positivos divisibles por \( 9 \) de cuatro dígitos hay tales que los dígitos que los componen no son cero y no son divisibles por \( 3 \)?
How many positive four-digit numbers divisible by \(9 \) are there such that the digits that compose them are not zero and are not divisible by \(3 \)?
S8
Para que un número de cuatro dígitos, digamos \( n=abcd \), sea divisible por \( 9 \) se tiene que \( a+b+c+d=9k \). El menor valor que puede tomar \( 9k \) es \( 9 \) y el mayor \( 27 \).
Una pequeña exploración muestra que las únicas posibilidades para obtener \( 9 \) son:
\begin{eqnarray}
9&=&1+1+2+5,\\
9&=&2+2+1+4
\end{eqnarray}
Lo anterior debido a que los dígitos \( a,b,c,d \not\in \lbrace0,3,6,9 \rbrace \)
Análogamente las posibilidades para obtener \(18\) son
\begin{eqnarray}
18&=&1+1+8+8,\\
18&=&2+2+7+7,\\
18&=&4+4+5+5,\\
18&=&2+4+4+8,\\
18&=&1+5+5+7,\\
18&=&1+2+7+8,\\
18&=&1+4+5+8,\\
18&=&2+4+5+7.
\end{eqnarray}
Por último las opciones para obtener \(27\) son
\begin{eqnarray}
27&=&4+7+8+8,\\
27&=&5+7+7+8
\end{eqnarray}
Observe que las ecuaciones \( (1),(2),(6),(7),(11) \) y \( (12) \) contienen un sólo dígito repetido y por cada ecuación de estas debemos permutar los dígitos tenemos así \( \frac{4!}{2!}=\frac{24}{2}=12 \). Por lo tanto, la cantidad de números \( abcd \) divisibles por 9 con dos dígitos iguales y la condición dada son \( 6\times 12=72 \).
Por otro lado, las ecuaciones \( (3),(4) \) y \( (5) \) muestran los números buscados usando solo dos dígitos, es decir, hay dos repeticiones y las posibles permutaciones en cada una de estas ecuaciones es \( \frac{4!}{2!2!}=\frac{24}{2\times 2}=6 \). Así que hay \(3 \times 6=18 \) números con las condiciones pedidas y que tienen dos dígitos repetidos.
Por último, las ecuaciones \( (8),(9) \) y \( (10) \) muestran los números buscados con todos los dígitos distintos de estos hay \( 4!=24 \) y por tanto hay un total \(3 \times 24=72\) números con las condiciones pedidas y que tienen dos dígitos repetidos.
Resumiendo el total de números de cuatro dígitos tal que ninguna de las cifras que lo componen son divisibles por \(3\) o son cero es \(72+18+72=162\).
P9 (UDENAR)
El rectángulo $ABCD$ tiene área $120$ cm$^2$. El punto $E$ satisface que $\overline{AD}=2\overline{ED}$ y $F$ es un punto sobre $\overline{BC}$. Si se conoce que las áreas de los triángulos $EGD$ y $ABH$ son $12$ cm$^2$ y $10$ cm$^2$ respectivamente, ¿cuál es el valor del área en centímetros cuadrados del cuadrilátero $EHFG$? (no escriba unidades en su respuesta)
The rectangle $ABCD$ has area $120$ cm $^ 2$. The point $E$ satisfies that $\overline {AD} = 2 \overline {ED}$ and $F$ is a point on $\overline {BC}$. If the areas of the triangles $EGD$ and $ABH$ are known to be $12$ cm $^ 2$ and $10$ cm $^ 2$ respectively, what is the value of the area in square centimeters of quadrilateral $EHFG$? (do not write units in your answer)
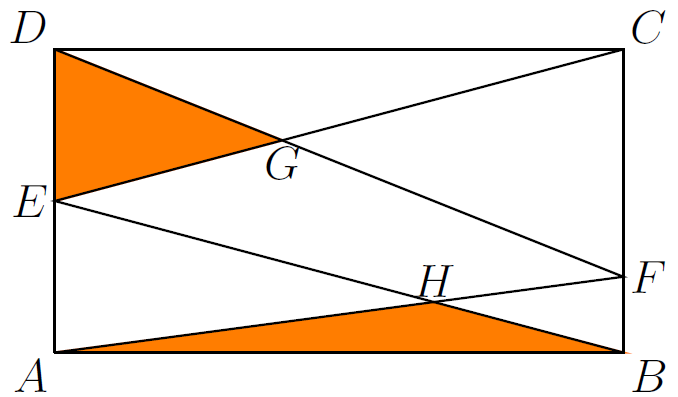
S9
Primero observemos que las áreas de los triángulos $BCE$ y $AFD$ son la misma ya que tienen igual base y altura. Por lo tanto,
\begin{equation*}
A(\triangle AFD)=A(\triangle BCE)=\dfrac{\overline{BC}\times\overline{CD}}{2}=\dfrac{120}{2}=60 \ \text{cm}^2.
\end{equation*}
Por otro lado, dado que $\overline{AE}=\overline{ED}$ se tiene
\begin{equation*}
A(\triangle ABE)=A(\triangle ECD)=\dfrac{\overline{ED}\times\overline{DC}}{2}=\dfrac{\overline{AD}\times\overline{DC}}{4}=\dfrac{120}{4}=30 \ \text{cm}^2.
\end{equation*}
De esta manera se obtiene que
\begin{equation*}
A(\triangle AHE)=A(\triangle ABE)-A(\triangle ABH)=30-10=20 \ \text{cm}^2,
\end{equation*}
y así
\begin{equation*}
A(EHFG)=A(\triangle AFD)-A(\triangle AHE)-A(\triangle EGD)=60-20-12=28 \ \text{cm}^2.
\end{equation*}
P10 (UNIQUINDIO)
Si \(a\) y \(b\) son números enteros cuyo producto es \(6\), ¿cuál es el menor valor posible de \(a^b\)?
If \(a\) and \(b\) are whole numbers whose product is \(6\), what is the smallest possible value of \(a^b\)?
S10
Tenemos que las parejas ordenadas donde se cumple este es
\(a=1\) y \(b=6 \Rightarrow(1,6)\)
\(a=6\) y \(b=1 \Rightarrow(6,1)\)
\(a=-1\) y \(b=-6 \Rightarrow(-1,-6)\)
\(a=-6\) y \(b=-1 \Rightarrow(-6,-1)\)
\(a=3\) y \(b=2 \Rightarrow(3,2)\)
\(a=2\) y \(b=3 \Rightarrow(2,3)\)
\(a=-3\) y \(b=-2 \Rightarrow(-3,-2)\)
\(a=-2\) y \(b=-3 \Rightarrow(-2,-3)\)
En consecuencia, el menor valor de la potencia \(a^b\) es
\(a^{b}=\left(-6\right)^{-1}=\frac{1}{\left(-6\right)^{1}}=-\frac{1}{6}\)
P11 (UIS)
¿Cuál es el residuo que deja el número $\underset{333\ unos}{\underbrace{111\dots 11}}$ cuando se divide entre \(15\)?
What is the remainder of the number $\underset {333\ ones}{\underbrace{111\dots11}} $ when divided by \(15\)?
S11
Note que
$$\underset{333\ unos}{\underbrace{111\dots 11}}=\underset{331\ unos}{\underbrace{111\dots 11}}05+{\bf 6}$$
y el número \(\underset{331\ unos}{\underbrace{111\dots 11}}05\) es múltiplo de \(15,\) ya que es múltiplo de \(5\) (pues termina en \(5\)), y es múltiplo de \(3\) (pues la suma de sus cifras es \(331+5=336\) que es múltiplo de \(3\)). Por lo tanto el residuo que se obtiene al dividir $\underset{333\ unos}{\underbrace{111\dots 11}}$ entre \(15\) es \(6.\)
P12 (LUZ)
Sea \( S(n)\) la suma de los dígitos del entero positivo \( n\). Halle el mayor entero \( N \) de cuatro dígitos tal que \( S(N+234) = S(N)\).
Let \(S(n)\) be the sum of the digits of the positive integer \(n\). Find the largest four-digit integer \(N\) such that \(S(N+234)=S (N)\).
S12
\(S(N+234)\) es igual a \(S(N) + S(234) - 9c\), donde \(c\) es el número de acarreos o llevadas realizadas al sumar \(N+234\). Luego \(S(N+234) = S(n)\) equivale a \(S(234) - 9c = 0\), es decir a \(c = 1\). Para obtener el mayor \(N\) posible de cuatro dígitos comenzamos por poner 9 en las unidades de 1000. Ahora no puede haber acarreo en las centenas pues habría un segundo acarreo en las unidades de 1000. Luego el dígito más grande posible en las centenas es 7. Ahora no puede haber acarreo en las decenas pues también los habría en las centenas y en las unidades de 1000. Entonces la única posibilidad de acarreo que nos queda es en las unidades, y ponemos 9 como dígito de las unidades. En las decenas el mayor dígito que podemos poner es 5, pues con 6 o más habría otro acarreo en las decenas. Luego el mayor \(N\) posible es 9759.
2. (------)
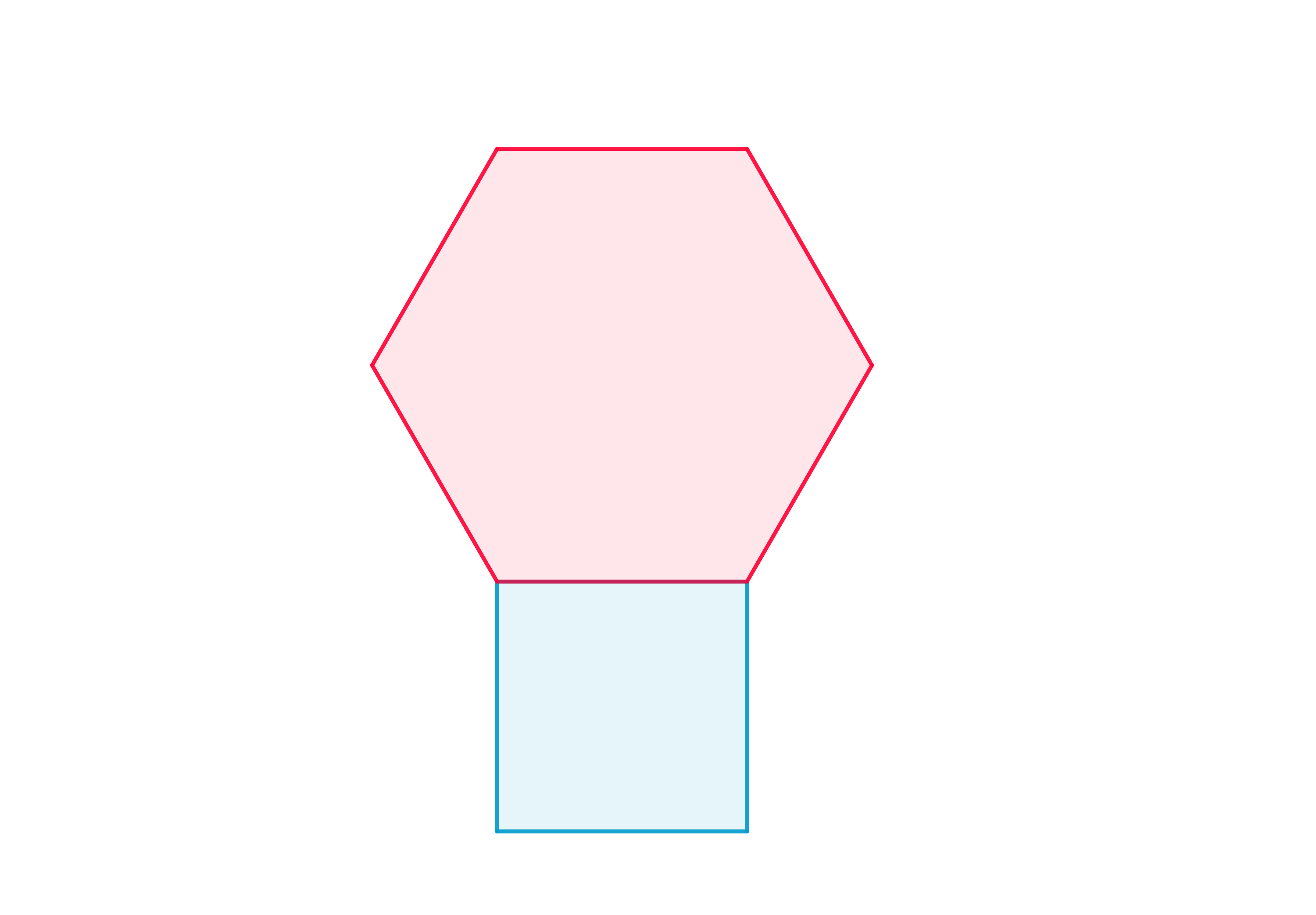
Solución
Sea \( r \) la medida del lado compartido por el hexágono y el cuadrado, tenemos que el área del cuadrado es \( B=r^2 \) y el área del hexágono es \( 6 \) veces el área de un triángulo equilátero de lado \( r\).

Usando el teorema de Pitagoras obtenemos que la altura de este triángulo es \( \dfrac{\sqrt{3}r}{2} \). Así el área de cada triángulo es \( \dfrac{\sqrt{3}r^2}{4} \) y el área del hexágono es \( A=\dfrac{3\sqrt{3}r^2}{2} \). Concluimos que \( \dfrac{A}{B} = \dfrac{3\sqrt{3}}{2} \).
3. (-----)
Un medicamento cuesta \(\$120\). Luego de una disminución del precio, el número de compradores se aumentó en la mitad y el dinero recaudado por la venta aumentó en una cuarta parte. ¿En cuánto se disminuye el precio del medicamento?
A drug costs \(\$120\). After a price decrease, the number of buyers was increased by half and the money raised from the sale increased by a quarter. How much is the price of the medicine reduced?
Solución
Sea \(P\) el precio inicial, \(C\) el numero de compradores y \(d\) el descuento. Se tiene: \(PC = 12000\quad \mbox{y}\quad C\left(1+ \frac{1}{2}\right)P(1-d)= 12000\left(1+ \frac{1}{4}\right).\) Reemplazando \(PC\) en la segunda ecuación, se tiene que \(d\) es \(\frac{1}{6}\) y por ello el descuento fue de \(\frac{1}{6} (12000)=200\), que es la respuesta.
4. (-----)
La menor distancia entre las localidades \(A\) y \(B\) separados por \(5\) montañas encadenadas (una seguida de la otra) que forman triángulos equiláteros con la horizontal es de \(14\) kilómetros. ¿Cuál es la distancia que se debe recorrer sobre las montañas para ir de \(A\) hasta \(B\) y regresar?

The smallest distance between the localities \(A \) and \(B \) separated by \(5 \) chained mountains (one followed by the other) that form equilateral triangles with the horizontal is \(14 \) kilometers. What is the distance that must be traveled over the mountains to get from \(A \) to \(B \) and back?
Solución
Como cada triángulo es equilátero, sus lados miden igual. Por lo tanto, ir de \(A\) a \(B\) sobre las montañas es igual al doble de la distancia horizontal, es decir, 28 kilómetros. Como la pregunta es sobre la distancia de \(A\) a \(B\) ida y regreso sobre las montañas, entonces la respuesta es 56 kilómetros.
5. (-----)
Determine el valor de la variable \(e\) en la siguiente tabla, de modo que la tabla resultante sea un Cuadrado Mágico (es decir, que todas sus filas, columnas y diagonales sumen igual):
| \(1\) | \(15\) | \(14\) | \(4\) |
| \(a\) | \(b\) | \(7\) | \(9\) |
| \(c\) | \(d\) | \(11\) | \(5\) |
| \(e\) | \(f\) | \(g\) | \(h\) |
Determine the value of the variable \(e\) in the following table, such that the resulting table is a Magic Square (i.e. the sum of all its rows, columns and diagonals are equal):
| \(1\) | \(15\) | \(14\) | \(4\) |
| \(a\) | \(b\) | \(7\) | \(9\) |
| \(c\) | \(d\) | \(11\) | \(5\) |
| \(e\) | \(f\) | \(g\) | \(h\) |
Solución
Solución 1:
Como la tabla arriba indicada es un Cuadrado Mágico la suma de sus filas, columnas y diagonales son iguales. Es decir, suman \(34\). Luego tenemos que:
\[\begin{align*}h + 5 + 9 + 4 &=34\\ h &= 16\end{align*}\]
De igual forma \(g=2\) y tenemos la siguiente tabla:
| \(1\) | \(15\) | \(14\) | \(4\) |
| \(a\) | \(b\) | \(7\) | \(9\) |
| \(c\) | \(d\) | \(11\) | \(5\) |
| \(e\) | \(f\) | \(2\) | \(16\) |
De esta última tabla podemos ver que
\[\begin{align*} b+1+11+16&=34 \\ b&=6 \end{align*}\]
Además,
\[\begin{align*} a&=34-22\\ a&=12 \end{align*}\]
Resultando la tabla:
| \(1\) | \(15\) | \(14\) | \(4\) |
| \(12\) | \(6\) | \(7\) | \(9\) |
| \(c\) | \(d\) | \(11\) | \(5\) |
| \(e\) | \(f\) | \(g\) | \(h\) |
Por último, usando la información en la última tabla tenemos el sistema de ecuaciones:
\[\begin{align*} c+d&=34-16\\ c+d&=18 \end{align*}\]
\[\begin{align*} e+f&=34-18\\ e+f&=16 \end{align*} \]
\[\begin{align*} c+e&=34-13\\ c+e&=21\end{align*}\]
\[\begin{align*} d+f&=34-21 \\ d+f&=13\end{align*}\]
\[\begin{align*} e+d&=34-11\\ e+d&=23 \end{align*}\]
De las ecuaciones \(d+e=23\) y \(e+f=16 \) tenemos
\[\begin{align*} d-f&=7 \end{align*}\]
De las ecuaciones \(d+f=13\) y \(d-f=7\), se tiene
\[\begin{align*} 2d&=20\\ d&=10\end{align*}\]
De donde se obtiene que \(f=3\), \(c=8\) y \( e=13\).
Solución 2:
Como la tabla es un Cuadrado Mágico, podemos utilizar el algoritmo para resolver un cuadrado mágico \(4\times 4\) de la siguiente manera.
Se ubican los números del del \(1\) al \(16\) en su orden en la tabla, como sigue:
| \(1\) | \(2\) | \(3\) | \(4\) |
| \(5\) | \(6\) | \(7\) | \(8\) |
| \(9\) | \(10\) | \(11\) | \(12\) |
| \(13\) | \(14\) | \(15\) | \(16\) |
Luego los números en las casillas en blanco se intercambian en parejas de la siguiente forma: \(2\) y \(15\); \(3\) y \(14\); \(5\) y \(12\) y \(8\) y \(9\). Obteniendo la tabla:
| \(1\) | \(15\) | \(14\) | \(4\) |
| \(12\) | \(6\) | \(7\) | \(9\) |
| \(8\) | \(10\) | \(11\) | \(5\) |
| \(13\) | \(3\) | \(2\) | \(16\) |
De donde se obtiene que $ a=12$, $ b=6$, $ c=8$, $ d=10$, $ e=13$, $ f=3$, $ g=2$ y $ h=16$.
6. ()
Juan dibujó un rectángulo que al restarle \(6\) unidades a la base y sumarle \(4\) unidades a la altura se convierte en un cuadrado que tiene la misma área del rectángulo. ¿Cuál es el área rectángulo inicial?
Juan drew a rectangle such that when subtractiing \(6\) units to the base and adding \(4\) units to the height it becomes a square with the same area as the rectangle. What is the area of the initial rectangle?
Solución
Sea \(x\) la base y \(y\) la altura del rectángulo original. Entonces se tiene que
\[(*)\ \ \ \ \ \ x-6=y+4\]
\[(**)\ \ \ \ \ \ xy=(x-6)^{2}\]
De la ecuación \((*)\) se tiene que \(x=y+10,\) de modo que de la ecuación \((**)\) se obtiene \((y+10)y=(y+4)^{2},\) de donde se concluye que \(y=8\) y \(x=18.\) Área del rectángulo es \(8\times 18=144\ u^2.\)
7. ()
Determinar el valor del ángulo marcado con \(\alpha\) en la siguiente figura, sabiendo que \(ABCDEFGHIJ\) es un decágono regular.
Determine the value of the angle marked with \(\alpha\) in the following figure, knowing that \(ABCDEFGHIJ\) is a regular decagon.
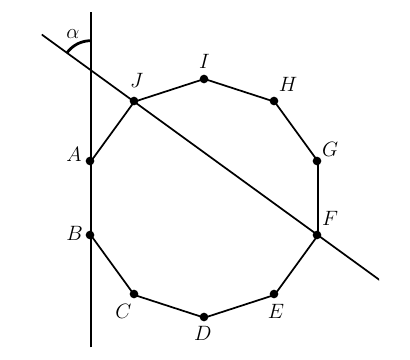
Solución
Considere la siguiente figura en la que \(P\) es la intersección del segmentos \(\overline{ID}\) y \(\overline{JF}\)
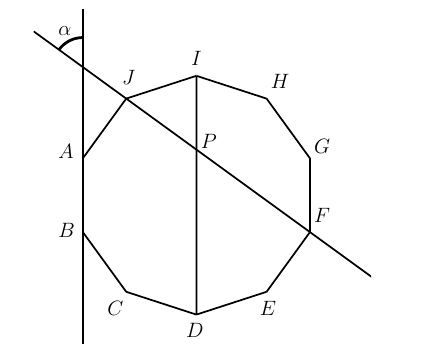
Note que el segmento \(\overline{GF}\) es paralelo a la recta que contiene los puntos \(A\) y \(B\) , luego el ángulo \(\alpha\) es congruente con el ángulo \(GFJ\) por ser ángulos correspondientes entre paralelas. Sabemos que la medida de cada ángulo interno en un decágono regular es \(144°\), y teniendo en cuenta que al trazar todas la diagonales desde un vértice de un polígono regular con \(n\) lados, el ángulo interno del polígono correspondiente a este vértice queda dividido en \(n-2\) ángulos congruentes, se concluye que \(\measuredangle GFJ=\dfrac{144}{8}\times 3=54º\) . Por lo tanto \[\alpha=\measuredangle GFJ=54º.\]
8. ()
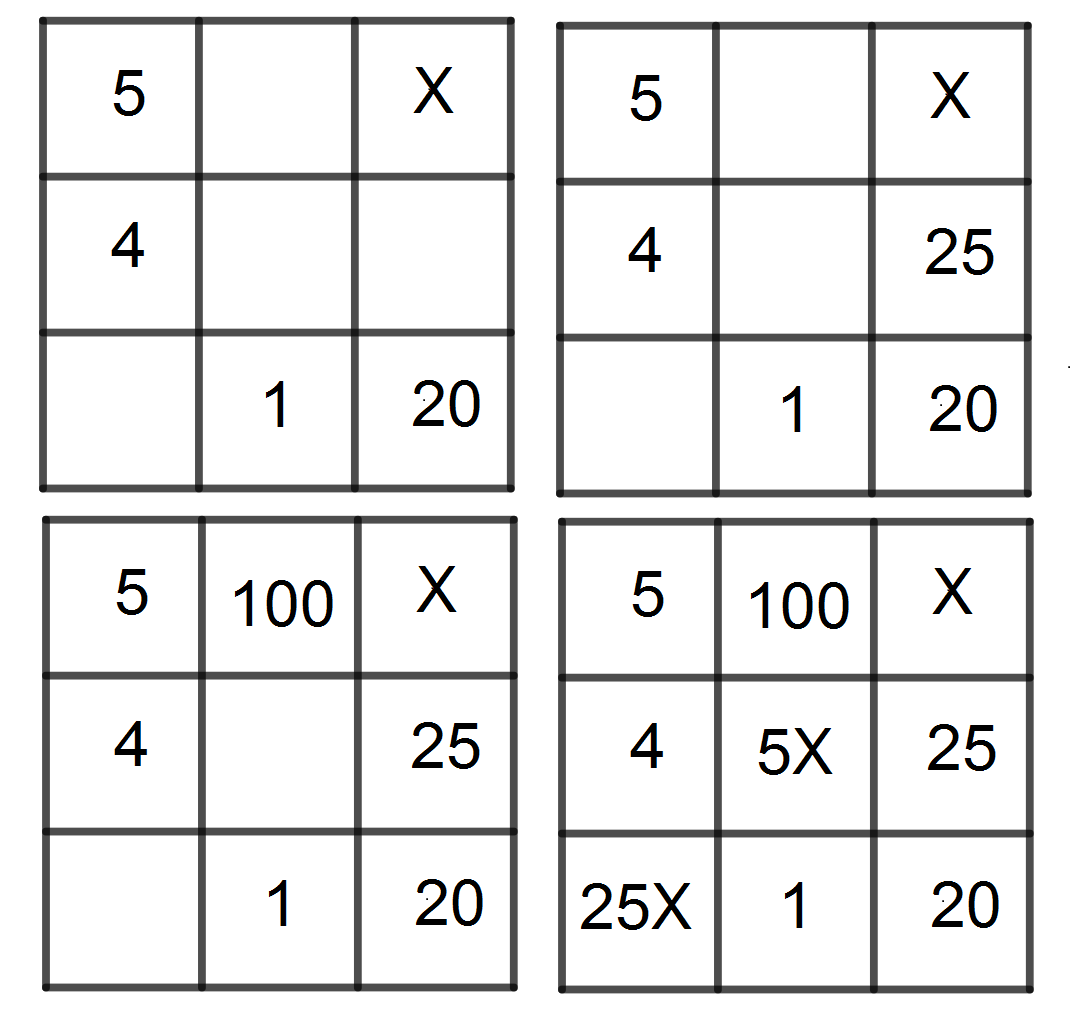
Un cuadrado mágico multiplicativo es tal que el producto de los números en cada fila, columna y diagonal es el mismo. Si las casillas del cuadrado del diagrama se llenan con enteros positivos de modo que se forma un cuadrado mágico multiplicativo, ¿cuál es el valor de $X$?
A multiplicative magic square is such that the product of the numbers in each row, column and diagonal is the same. If the entries in the square are filled with positive integers in such a way that a multiplicative magic square is formed, what is the value of $X$?
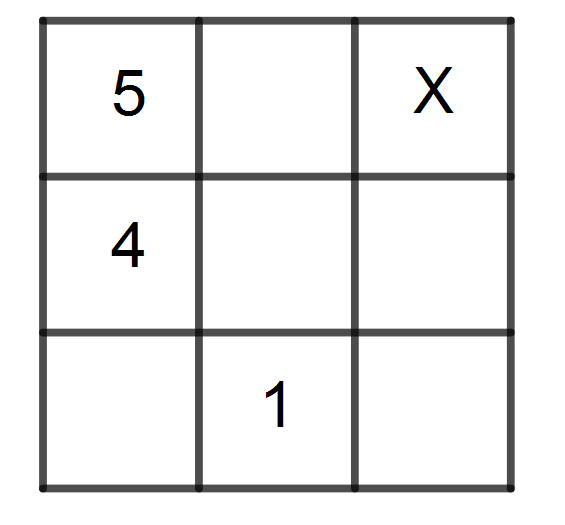
9. ()
Se definen las siguientes dos operaciones en los enteros: \(a\circ b= a-b\) y \(a\star b= 3^a+b^4\), calcule \((4\circ 2)\star 3\).
The following two operations are defined in the integers: \(a\circ b= a-b\) and \(a\star b= 3^a+b^4\), calculate \((4\circ 2)\star 3\).
10. ()
Un número de más de tres cifras se dice que tiene la propiedad Fibonacci si cada dígito a partir del tercero es la suma de los dos anteriores. Por ejemplo, el \(1347\) tiene la propiedad Fibonacci, pues el tercer dígito es \(4=1+3\), y el cuarto es \(7=3+4\). Encontrar la suma de los dígitos del número más grande con la propiedad de Fibonacci.
A number with more than \(3\) digits is said to have the Fibonacci property if each digit starting from the third is the sum of the two previous digits. For example, \(1347\) has the Fibonacci property, since the third digit is \(4=1+3\), and the fourth is \(7=3+4\). Find the sum of all the digits of the largest possible number with the Fibonacci property.
Solución
Notemos que los dígitos van creciendo, pues son la suma de los dos anteriores. Así que, para que un número tenga muchos dígitos se necesita que la suma de los dos primeros dígitos sea lo más pequeña posible. Esto se logra cuando el primer dígito es 1 y el segundo es 0 así el numero es
10112358 cuya suma de dígitos es $1+0+1+1+2+3+5+8=21$.
Observamos que la siguiente suma más pequeña para el tercer dígito es 2, los posibles números son $202246$ y $112358$. Así que si se hace que el tercer dígito sea más grande, la suma crece rápidamente y no hay ningún otro con 8 dígitos, por tanto es el más grande.
11. ()
Considere la sucesión de todos los números binarios de \(6\)-dígitos, donde cada uno de los \(6\) dígitos es \(1\) o \(0\). Por ejemplo:
| \(000000\) |
| \(100000\) |
| \(010000\) |
| \(\vdots\) |
| \(111110\) |
| \(111111\) |
Determine cuántos elementos poseen más \(1\)'s que \(0\)'s.
Consider the sequence of all \(6\)-digit binary numbers, where each of the \(6\) digits is \(0\) or \(1\). For example:
| \(000000\) |
| \(100000\) |
| \(010000\) |
| \(\vdots\) |
| \(111110\) |
| \(111111\) |
How many of them have more \(1\)'s than \(0\)'s?
Solución
Solución 1:
Los elementos de la sucesión que poseen más \(1\)'s que \(0\)'s son los que poseen de a cuatro, cinco o seis \(1\)'s. Luego
\[\begin{align*} \binom{6}{4} &= 15\longrightarrow \text{ Cantidad de elementos con cuatro } 1\text{'s} \\ \binom{6}{5} &= 6\longrightarrow \text{ Cantidad de elementos con cinco } 1\text{'s}\\ \binom{6}{6} &= 6\longrightarrow \text{ Cantidad de elementos con seis } 1\text{'s}\\ \end{align*} \]
Por tanto, la cantidad de elementos que poseen más \(1\)'s que \(0\)'s son \(15+6+1=22\).
Solución 2:
La cantidad de elementos en total que tiene la sucesión es \(2^6=64\). Ahora, la cantidad de elementos que tienen igual número de \(1\)'s y \(0\)'s es \({{6}\choose{3}}=20\).
Por simetría la cantidad de elementos que poseen más \(1\)'s que \(0\)'s es la misma cantidad de elementos que poseen más \(0\)'s que \(1\)'s. Por tanto, el número de elementos que tienen más \(1\)'s que \(0\)'s:
\[\frac{2^6 - {{6}\choose{3}}}{2} = \frac{64-20}{2} = \frac{44}{2}=22\]
12. ()
Mi clave del banco es "anti-hackers" y consta de siete dígitos que forman un número capicúa, es decir se lee igual de derecha a izquierda que de izquierda a derecha. El primero y los dos últimos dígitos corresponden respectivamente al mes y al día del cumpleaños de mi madre y los tres dígitos del centro (tercera, cuarta y quinta posición) forman un número que es el producto del mes y del día. Si el día del cumpleaños de mi madre es número primo, adivina cuál es la clave que uso.My password at the bank is "anti-hacker" and is made up of seven digits that form a capicúa number, that is, it reads the same from left to right than from right to left. The first and last two digits correspond to the day and month of my mother's birthday and the three middle digits (third, fourth y fifth position) form a number that is the product of that month and day. If the day of my mother's birthday is a prime number, guess my password.

Solución
La clave tiene siete dígitos, enumeramos la posición de cada dígito así: