Solucionario COMATEQ 2019
Agradecemos a las universidades que contribuyeron enviando problemas al banco: ULA, UIS, UDENAR, UDO, UNIVALLE, LUZ, UT, UPRM, UDEA.
1. (UDENAR)
Se desea pintar cada rectángulo de una cuadrícula $5\times5$, usando los colores amarillo, azul, rojo y verde. Con la distribución inicial de colores en la figura dada, ¿cuáles colores podrían estar en la casilla con interrogante, si ningún rectángulo de la cuadrícula puede compartir vértices, ni lados con casillas de igual color?
You want to paint each rectangle of a $5\times5$ grid, using the colors yellow, blue, red and green. With the initial distribution of colors in the given figure, which colors could be in the box with question mark, if no rectangle of the grid can share vertices, or sides with squares of the same color?
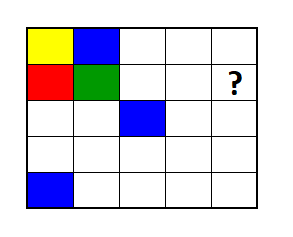
Solución
Observe que la casilla en la fila 3, columna 2, comparte con los colores rojo y azúl un vértice y con el verde un lado. De aquí dado que esta casilla ya comparte con tres colores, la única opción para rellenarla es con amarillo.
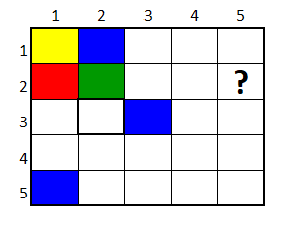
De forma similar, se tiene que la casilla en la fila 2, columna 3, comparte vértices y lados con los colores azúl, verde y amarillo. Por lo tanto, como esta casilla comparte con tres colores, solo se puede rellenar con color rojo.
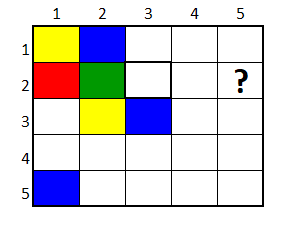
Continuando de forma análoga, la casilla en la fila 1, columna 3, se rellena con amarillo.
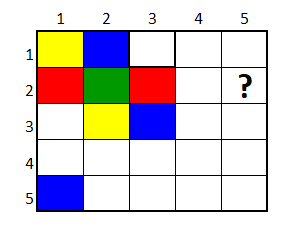
Repitiendo el proceso descrito, se encuentra que la casilla con interrogante se completa con el color rojo.
Note que se debe tener cuidado al concluir la respuesta de inmediato, pues una condición del problema es que a partir de la distribución inicial se debe rellenar totalmente la cuadrícula con los cuatro colores.
Continuamos rellenando la cuadrícula, al pintar de azúl la casilla en la fila 3, columna 1.
Finalmente, manteniendo la idea propuesta se rellena toda la cuadrícula y se confirma que la casilla con interrogante es roja.
5. (UNIVALLE)
Considere el siguiente círculo y hexágono regular (con sus seis lados congruentes) tal como se muestra en la figura.
Consider the following circle and regular hexagon (six congruent sides) as it is shown in the picture.
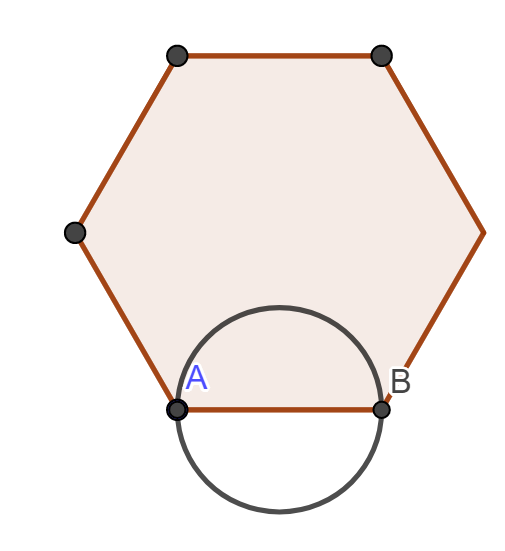
El segmento $AB$ es a su vez un lado del hexágono y un diámetro del círculo. Sean $a$ y $b$ las áreas del círculo y del hexágono, respectivamente. ¿El valor de la expresión $\frac{a}{b} $ es?
The segment $AB$ is a side of the hexagon and the diameter of the circle. Let $a$ and $b$ the areas of the circle and the hexagon respectively. What is the value of $\frac{a}{b} $ ?
Solución
Sea $R$ el radio de la círculo, por tanto el lado del hexágono es $2R$. Tenemos que el área del circulo es $b = \pi R^2$. Para calcular el área del hexágono dividamos el hexágono en seis triángulos equiláteros congruentes entre sí.
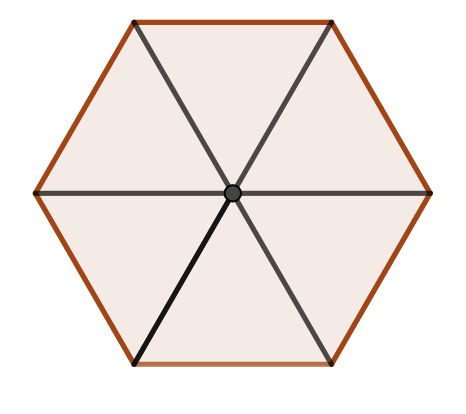
Por tanto, el área del hexágono es calcular seis veces el área del triángulo equilátero de lado $2R$. Sea $X$ la altura de uno de los seis triángulos por Teorema de Pitagóras obtenemos $4R^2 = R^2 + X^2$, es decir, $X = \sqrt{3}R$.
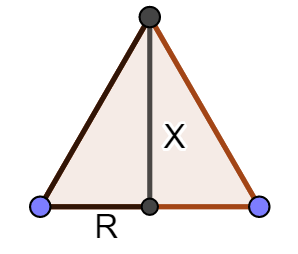
Por tanto, el área del triángulo equilátero es $\sqrt{3}R^2$ y el area del hexágono $b = 6\sqrt{3}R^2$.
Concluimos que $\frac{a}{b} = \frac{\pi R^2}{6\sqrt{3}R^2} = \frac{\pi }{6\sqrt{3}}$.
8. (UNIVALLE)
Mónica quiere visitar a su amiga Karen en su nuevo apartamento, para ello sigue las indicaciones de su amiga: Viajar primero al norte 10 metros, girar a la derecha 10 metros y continuar siempre girando a la derecha en la siguiente sucesión $20\;$ metros, $20\;$ metros, $30\;$ metros, $30\;$ metros, ... hasta completar $2400\;$ metros ¿Cuántas veces giró Mónica a la derecha?
Mónica wants to visit her friend Karen at her new apartment, in order to do that, she follows her friend instructions: To travel first north, 10 meters, turn right 10 meters and continue turning right in the following way: $20\;$ meters, $20\;$ meters, $30\;$ meters, $30\;$ meters, ... in this way until you complete $2400$ meters. How many times did Monica turn right?
Solución
La figura muestra la forma del recorrido de Mónica:
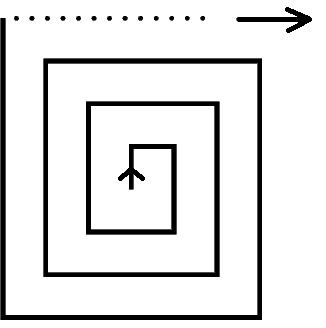
Para saber la cantidad de giros de Mónica debemos resolver la ecuación
\begin{eqnarray*}
10+10+20+20+ \cdots +10n+10n&=&2400 \\
10(1+1+2+2+\cdots +n+n)&=&2400\\
10 \times 2(1+2+3+\cdots n)&=&2400\\
10 \times 2 \times \frac{n(n+1)}{2}&=&2400
\end{eqnarray*}
Esta última ecuación es equivalente a
\begin{eqnarray*}
n(n+1)&=&240\\
n^2+n&=&240\\
n^2+n-240&=&0
\end{eqnarray*}
Usando la formula cuadrática tenemos que $n=15$ o $n=-16$. Tomamos la solución positiva y así tenemos $n=15$, esto es en total hace $2*15-1=29$ giros a derecha.
9. (UDENAR)
Sea $ABC$ un triángulo de área $4$ cm$^2$. Suponga que $\overline{AC}$ se divide en cuatro partes iguales, con segmentos paralelos a $\overline{AB}$. Determine el área en cm$^2$ de la región sombreada, si las líneas punteadas son paralelas a $\overline{BC}$. No escriba las unidades en su respuesta.
Let $ABC$ be a triangle with an area of $4$ cm$^2$. Assume that $\overline{AC}$ is divided in four equal parts, with segments parallel to $\overline{AB}$. Determine the area in cm$^2$ of the shaded region, if the dotted lines are parallel to $\overline{BC}$. Do not write the units in your answer.
